Dodwell: The Obliquity of the Ecliptic
CHAPTER 3 ANCIENT CHINESE OBSERVATIONS
Our knowledge of the Chinese astronomical observations is largely due to P. Gaubil, S.J. (1689-1759 A.D.), who was a French missionary in China. He extracted a considerable number of Chinese solstitial observations from numerous documentary sources. He studied these very thoroughly, and communicated them to European astronomers in his Edifying Letters, published by Souciet in 1732. According to Leopold de Saussure, “the Missionary P. Gaubil, S.J., who took so much trouble to inform European astronomers in regard to Chinese astronomy, was of an enquiring mind, modest, and of great honesty.” In 1734 P. Gaubil sent an important manuscript to the French astronomer De Lisle, giving the results of his astronomical researches concerning the constellations and the Chinese catalogues of the fixed stars, the cycle of days, the solstices, and the meridian shadows of the gnomon observed in China. Seventy-five years later, in the beginning of the 19th century, Laplace, recognizing the unique value of this work, rescued it from oblivion and published, in the French Connaissance des Temps for 1809, the portion dealing with the solstices and the meridian shadows of the gnomon observed in China. Altogether, the Chinese solstitial observations which are available consist of a valuable series of 26 observations of the mid-day altitudes of the sun at the summer and winter solstices, extending over 2380 years from 1100 B.C. to 1280 A.D. They were regarded as important observations from the Chinese point of view, and were made by official astronomers of the various periods, several of whose names have come down to us. Also, they were made at the capital cities of China or residences of the sovereign in the different dynasties. This fact throws a favorable light on the accuracy of the observations, because the latitudes derived from them are in remarkable agreement with the true latitudes of those capitals. These were:
All these observations, with the exception of the observations made by Ko-chou-King at Peking in the days of Kublai Khan, were made with the vertical gnomon, fixed by law in China at a standard height of 8 Chinese feet, which was equal to 8 feet 9 inches in English measure. Ko-chou-King, in an attempt to obtain the greatest possible accuracy, used a gnomon 40 feet in height, with a plate of copper at the top, pierced with a small hole, so as to give a round spot of light, the center of which was accurately measured, and the length of the shadow precisely recorded.
We may ask, why was such careful attention given to the measurement of the solar shadows over so long a period of Chinese history? The answer given by P. Ricci is that the Chinese in their social, religious and governmental system, attached special importance to the Calendar and to the celestial observations necessary for maintaining it accurately.(1) This was because the Chinese civil year was a lunar one, and did not fit in with the seasons. All changes in the sky were considered to have a direct influence on terrestrial life, and were carefully observed. The astronomical seasons, with the accompanying changes in vegetation, were the most obvious, and “the harmonious relationship existing between heaven and earth was considered to extend even to the domain of morals.” It was the chief duty of the Emperor “to make known the conditions of this harmony, i.e., to indicate the limits of the seasons, and the situation of the terrestrial or civil year with regard to the celestial or astronomical year.” For this purpose he employed numerous astronomers who were responsible to him for making the observations and for calculating the ephemerides. The Emperor, on his part, was held to be “responsible to heaven, and if he neglected the calendar, he not only caused inconvenience to the people, but was considered guilty of an irreverence which diminished his virtue and endangered the dynasty.” Necessity was thus laid both upon the Emperor and his ministers and astronomers to ensure that the observations were made as carefully as possible, and that they were maintained throughout the ancient and mediaeval eras. P. Ricci stated in 1605 A.D. that the Chinese King kept more than 200 people at great expense to calculate the ephemerides each year. The earliest Chinese astronomical observations are contained in the Chou-Pei-Soan-King ("the sacred book of calculations called Chou-Pei"). This book is a composite one, and is believed to have been first compiled in its present form in the 4th or 5th century B.C. The most ancient part gives results of observations made as far back as 1120 B.C., but a section relating to the observation of a circumpolar star (Suen-Ki), with which are associated meridian observations of the solar shadows at the summer and winter solstices, has been shown by the Chinese astronomer Kao-Kiun (formerly of the Zo-se Observatory, near Shanghai) to correspond with the date 700 B.C. A complete French translation of the Chou-Pei, with notes, was published by Edouard Biot in the Journal Asiatique, Paris, 1841. In a Chinese preface to the Chou-Pei, written in 1213 A.D., it is stated,
The word Pei technically signifies a vertical gnomon, and it appears from this statement that the Chou Pei was so named in honor of the celebrated prince Chou Kung, brother of Wu Wang (founder of the Chou dynasty, about 1120 B.C.), who is renowned in China through all the succeeding centuries for his wise legislation and interest in astronomical science. In the Chou-Pei results are given in two systems of measurement, circular and linear. The circular measurements give a larger value for the obliquity of the ecliptic, and are of an earlier date, probably about 1120 B.C. They are clearly based on measurements of the solar shadows at the summer and winter solstices. In the earliest part of the Chou-Pei where Chou Kung receives instructions from the grand prefect, Chang-Kao, it is stated that “the sky is measured in degrees.” The Chinese divided the circle into 365¼ degrees, each degree corresponding to the amount of the mean daily motion of the sun in the year. For finer measurement, the circle was also divided into 714,000 circular li. Thus each circular li was equivalent to approximately two seconds of arc, or 1/1800 of a degree (European). For purposes of calculation the Chinese subdivided the li into 300 pou. For further calculations used in connection with the celestial motions, the pou was divided into 1461 (i.e. 365¼ x 4) parts. Thus one Chinese degree was equivalent to 1954 li, 247 and 933/1461 pou. In the instructions given in the Chou Pei for drawing a circle (on a leveled platform) to represent the circle of the sky, it is said “to correspond with the circle of the sky, which is 365¼ degrees, divide carefully the circle traced on the ground. Let there not be the very smallest difference between the degrees.” Instructions are then given to divide this circle into four quadrants, and it is stated that “each of the four parts of the circumference will comprise 91 5/16 degrees.” The measurements are stated to have been made with the help of an officer called Ta-tsiang (grand carpenter). The earliest value of the obliquity of the ecliptic, afforded by the Chou Pei is indicated in the following terms:
Converting these figures into European degrees, we have:
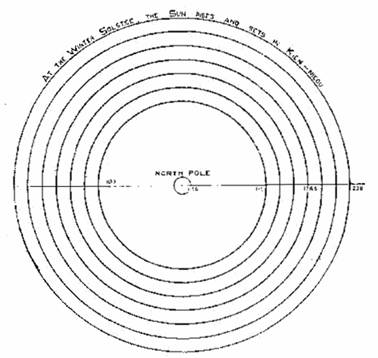
Thus both statements give the obliquity of the ecliptic at the earliest date of the Chou Pei (about 1120 B.C.) as 24 degrees 12 minutes 6 seconds. These most ancient Chinese results were obtained by calculation, based on observations made with the gnomon, and the method is stated in the text of the Chou Pei. A diagram is given of a polar projection of the sky, reproduced here (Fig. 6) , showing the “Seven Circles called Heng.”
Diagram of the Seven Circles called Heng
As it is stated in the commencement of the book that the sky is measured in degrees, and these degrees are also given values in circular li, at the rate of 714,000 li to 365¼ Chinese degrees (360 degrees European), it is clear that the projected radii of the Seven Circles represent circular measure. The inner circle of the group of seven, marked 119, is of 119,000 circular li radius, and is the polar projection of the circle of 60 degrees (European) north polar distance. (714000/119000 x 360° = 60°) The other circles are spaced at 10 degree intervals, namely, at polar distances of 70°, 80°, 90°, 100°, 110°, and 120°. The rule given in the text of the Chou Pei for obtaining the polar distances of the sun at the winter and summer solstices, is as follows:
This is then divided by the number of li and parts of a li equal to one Chinese degree, namely 1954 li 247 and 933/1461 pou. The result of this division gives 115°, 1695 li, 21 and 319/1461 pou, as previously stated (European, 114° 12’ 6”; and, subtracting 90°, the obliquity therefore is 24° 12’ 6”). In a similar manner, the rule given for the summer solstice is:
This is then divided by the number of li in one Chinese degree, as before; and the result of the division gives 66° 1481 li, 155 and 1245/1461 pou (European, 65° 47’ 54”, and, subtracting this from 90°, the obliquity is, as before, 24° 12’ 6”). The difference between 226,500 li, from *1 (the north polar distance of the Tropic of Capricorn), and 130,500 li, from *2 (the north polar distance of the Tropic of Cancer), gives for the total inter-tropical distance, or twice the angle of obliquity, 96,000 li (Chinese circular measure). This is equivalent to 48° 24’ 12” (European). From it we obtain the mean obliquity, 24° 12’ 6”. It must be clearly understood that these ancient calculations, which define the positions of the Tropics of Capricorn and Cancer, and therefore the obliquity of the ecliptic at that time, depended upon actual observations of the solar shadows cast by the vertical gnomon. There was no other way of knowing the solstitial positions of the sun except by these observations. They are referred to the date of about 1120 B.C. and were made at the ancient Chinese capital city of Mo. This city was situated on the western bank of the River Hoang-ho, in about latitude 35° 35’ N. and longitude 115° 40’ E. in what is now the province of Shantung. In Dr. Albert Hermann’s Historical and Commercial Atlas of China, (Volume 1, Monograph Series of the Harvard – Yen-Ching Institute, Harvard University Press, Cambridge, Massachusetts, U.S.A., 1935), there is a large scale map of this district, showing the original center of ancient China, with the seats of the dynasties and their B.C. dates, according to the traditional chronology. The City of Mo is shown as the seat of the Chang Dynasty, and was the royal residence from 1198 B.C. to 1122 B.C. The latitude of Mo, measured on this map, is 35° 35’ N., and it was about 16 miles north of the present town of Tsao-chow. This agrees with the time and route taken by Wu-Wang, first emperor of the Chou Dynasty, to travel with his army from his capital Hao-King (now Sian-fu). Having crossed the Hoang-ho River near Loyang, he advanced to the plain outside the capital city (i.e., Mo), of Chou, the last emperor of the Chang Dynasty, where the latter was defeated. Upon this he fled to his capital (Mo), set fire to his palace of Lou T’ai, and perished in the flames. (see Variétes Sinologiques, Shanghai, No. 52, pages 172, 173.) This obliquity of the ecliptic, obtained as above directly from the Chinese observations, described in the Chou Pei, viz. 24° 12’ 6”, was not corrected for refraction and solar parallax, which were unknown to the ancient observers. When these corrections are applied, the corrected obliquity of the ecliptic, given by the Chou Pei for about 1120 B.C., is 24 degrees 13 minutes 56 seconds. This is 24 minutes 17 seconds greater than the obliquity given by Newcomb’s Formula for the same date. The investigation of the errors of observation with the gnomon, given in the preceding Chapter 2, shows clearly that such a large difference, equivalent to three-quarters of the sun’s diameter, cannot possibly be explained as due to an error of observation. It is a real difference between the actually observed obliquity of the ecliptic at the date 1120 B.C. and the theoretical value calculated by means of Newcomb’s Formula. This result is to be specially noted because it is the earliest direct astronomical observation of the obliquity of the ecliptic that we have. The large difference from Newcomb’s Formula is confirmed by the lengths of the solar shadows at mid-day at the summer and winter solstices given in the later part of the Chou Pei, corresponding to the year 700 B.C. From these we get the obliquity of the ecliptic 24° 1’ 58”. This is 15’ 8” greater than the value for 700 B.C., calculated from Newcomb’s Formula. This difference is equivalent to half the solar diameter, and again it is far too large to be due to an error of observation with the gnomon. In addition, it is intermediate between the Chou Pei value for 1120 B.C. and the later series of Chinese observations, which fit closely on a curve, indicating the progressively increasing error of Newcomb’s Formula as we go backwards to ancient times. The following table illustrates the increasing change revealed by the Chinese observations as we go back into antiquity from 1280 A.D. to 1120 B.C. TABLE 2
Before leaving the Chinese observations, reference must be made to the shadow lengths (1.5 feet at the summer solstice, and 13.0 feet at the winter solstice, giving the obliquity 23° 54’ 4”), associated by Chinese tradition with the name of Chou Kung. These shadow lengths are found in the Chou Li (Book of Rites) and some other sources. It is clear, however, that they belong to a later date than that of Chou Kung. The internal evidence of the Chou Pei, together with the large progressive change in the obliquity of the ecliptic given by the Chinese observations over a period of 2300 years, shows that the earliest and largest value (24° 13’ 56”), obtained from the Chou Pei, belongs to the time of Chou Kung, about 1120 B.C. This is the date of the earliest recorded astronomical observation in China. Commenting on the shadow lengths 1.5 feet at the summer solstice, and 13.0 feet at the winter solstice, P. Gaubil wrote, “I have no doubt that observations were made from the time of Chou Kung, but I do not know if the figures which are given are very ancient.” (3) The late Dr. Villemarque, Director of the Zo-Se Observatory, near Shanghai, also expressed a similar opinion. In a letter to me on this subject, he wrote “Observations were certain about 1120 B.C., but the figures may have been altered in the course of the ages.” Some time after the downfall of the Chou Dynasty in 249 B.C., the Emperor Che Hwang-ti, of the Tsin Dynasty, moved by political reasons, ordered the burning of all books in China, except those relating to medicine, divination, and agriculture. This occurred in the year 213 B.C. After the fall of the Tsin Dynasty in 206 B.C., the emperors of the Han dynasty endeavored to restore Chinese literature. Their astronomers made fresh observations of the solar solstitial shadows, and it is stated that “during the Han Period (206 B.C. to 265 A.D.), the gnomon was perfected by terminating it with a plate of copper pierced with a small round hole. In place of the shadow of the edge, the centre of the luminous spot of light was observed.”(4) The Chinese astronomer Haui-Nan-Tzu (died B.C. 122) gave the shadow lengths 1.5 feet in summer and 13.0 feet in winter, as for his own time, say about 130 B.C. According to the New Curve, developed in this study, the obliquity of the ecliptic, corresponding to these figures, belongs more precisely to 295 B.C., i.e. 165 years before Haui-Nan-Tzu. But the difference in the shadow lengths for the two dates is not great, and it is possible that Haui-Nan-Tzu’s own measurements closely approximated to the figures which he gives. Two centuries after Haui-Nan-Tzu, it was represented to the Emperor Chang-ti, about 84 A.D., that calculation indicated certain errors in the Calendar, which gave erroneous values for the solstices, the equinoxes, and other dates. The Emperor, “having regard to these representations, ordered the astronomer Li-fong to make a new calendar. He did this, and gave it the name of Sse-fen, or four parts. The court was then at Loyang.” P. Gaubil says of this change: “The authors of the Sse-fen astronomy have marked for Loyang at the two solstices the shadows observed by Chou-Kung in the first observation, i.e., 1.5 feet summer solstice, and 13.0 feet winter solstice.... These authors supposed the observation made by Chou-Kung was unaltered.” This statement indicates that the Chinese were not aware of the changing value of obliquity in the course of time. Confusion was caused, also, by the difference in the length of the shadows according to the latitude of the place where the observations were made. On this account the Chinese observations need careful examination. In his notes, P. Gaubil writes that:
The confusion concerning the shadow lengths observed by Chou Kung seems to have originated after the burning of the books in the Tsin dynasty through which many of the old records wore lost, and it may be that the new value of the shadow lengths at Loyang after this event were ascribed to Chou Kung as a tribute of veneration for his memory. Concerning Chou Kung it is said that in addition to the observatory at which his astronomical observations were made, one was built also by his brother, the Emperor Wu Wang, founder of the Chou Dynasty. It was called
From the evidence now available we arrive at the conclusion that the shadow lengths of 1.5 feet in summer and 13.0 feet in winter, at Loyang, were obtained about the time of the “burning of the books” in the Tsin dynasty, or shortly after, in the Han Dynasty, and were ascribed to Chou Kung because of the veneration in which his name was held, and because it was thought the obliquity had remained unaltered since his time. The true value at the time of Chou Kung, however, is preserved in the Chou Pei. A careful analysis of all the available Chinese observations shows that the key to the difficulties mentioned by P. Gaubil lies in the value of latitude derived from the observations at the two solstices. In practically all cases, this is very close to the latitude of one or other of the ancient capitals of China, and confirms the general accuracy of the Chinese results. It can also be ascertained from the observations whether a plain gnomon casting a shadow, or one with a hole casting a luminous spot, was used. The examination of all the Chinese observations also confirms the accuracy of the large values of the obliquity of the ecliptic, obtained from the Chou Pei for the dates 1120 B.C. and 700 B.C. ********************
|