Part 4:  Foucault and the Rotating Mirror Experiments

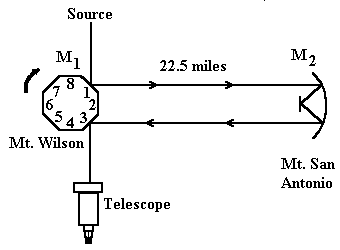
English, French, and Americans in Rotation
Foucault’s Rotating Mirror
Foucault’s Problems
Foucault’s Micrometer and c value
Enter the Americans
Newcomb’s Experiments
Newcomb's Problems
Newcomb’s Results
The Beginnings with Michelson
Michelson’s New Apparatus
Michelson’s Second Series Results
Michelson’s Third Series
Michelson’s Third Series Results
Michelson Tries Again
Details of the New Try
Results from the New Try
Michelson’s Series Five
Results from Series Five
Dorsey’s Comments
Michelson’s Last Experiment
Over to Pease and Pearson
Conclusions From Rotating Mirrors
Table 6: Rotating Mirror Experiments

English, French, and Americans in Rotation

In 1834, at 32 years of age, Sir Charles Wheatstone of England (1802-1875), after whom the electrical circuitry known as the Wheatstone Bridge is named, entered the discussion on the speed of light.  He was the first to suggest the method that incorporated a rotating mirror for the measurement of c.1  Unfortunately for the history of England in the debate about the value for c, Sir Charles’ suggestion was not taken up by his countrymen.  Instead, the French again led the way in pioneer experimentation, following which the lead came under American control.

Sir Charles’ suggestion regarding the rotating mirror was picked up four years later, in 1838, by the noted Parisian astronomer and physicist D.F.J. Arago (1786-1853).  (Arago is mainly remembered today for his work on the interference of polarized light, which he investigated in 1811, and electromagnetism in which he worked with Ampere (1775-1836).2  He also conducted experiments confirming diffraction that resulted from Resnel’s development of the wave theory of light.3  Arago polished the suggestion,4 which was then examined in detail by his collaborating French fellow scientists, Fizeau and Foucault, between 1845 and 1849.  Following a difference of opinion, Fizeau dropped out, leaving Foucault to pursue the issue independently.2a

Jean Leon Foucault (1819-1868), who preferred the name Leon, is remembered by the Foucault pendulum, whereby he demonstrated the rotation of the earth.  In optics, the Foucault knife-edge test bears his name, a test which many amateur astronomers use to try their concave mirrors for accuracy.  His association with Fizeau led him into dealings with light, and his doctoral thesis in 1851 comprised his research into the velocity of light in water.  One year prior to this, his study of the possibilities of the rotating mirror method led him to call attention to two inherent problems in 1850 and again in 1854.5  However, by 1862 he had overcome these difficulties sufficiently to obtain a pioneering result for c by the method that now bears his name.

Encouraged by Foucault’s success, Michelson followed on in the U.S.A. in 1878 with a series of experiments until 1926 with the same method.  His compatriot, Newcomb, also performed several determinations from about 1880 to 1883.  The final determination by a form of this method coupled with a toothed-wheel type of effect was performed by Pease and Pearson in California and reported in 1935.

Foucault’s Rotating Mirror   

The basic principle involved in the method is as follows: a source of light passes through a semi-transparent plate of glass and is reflected from the rotating mirror.  The reflected light is then focused through the lens onto a concave mirror, which returned the light to the rotating mirror.  If the rotating mirror is stationary, light is reflected back to the semi-transparent plate of glass, from which it is reflected to the observer.  If the mirror is set rotating, the image appears at E’ instead of E as R has moved through a small angle in the time taken for light to travel from R through L to M and back.  The distance EE’ depends on the rate of rotation of R, the distance RM, and also RGE.  Measuring the values of these quantities allows the value for c to be determined.  The basic equation is c = 2D ω/α where D is the distance RM, the angular velocity of the mirror is ω, and the angle α is that which the mirror has turned through to give the deflection EE’.6

Foucault used a plane glass disk that was silvered on one side and blackened on the other as his rotating mirror.  It was just 14 mm in diameter and mounted in a ring that was part of the vertical axis of a 24 vane turbine driven by compressed air.  The total air pressure was kept constant at 30 cm of water, to within 0.2 mm, and the air was delivered to the turbine by a regulated precision blower.  A continuous flow of oil at constant pressure lubricated all bearings.  A toothed disk performing two rotations per second under precision clockwork was used as a stroboscope for determining the speed of the mirror.  Though Foucault rotated the mirror at 500 turns per second,7 he stated that the mirror and the disk would keep in step within one part in 10,000 for minutes at a time when the mirror was rotating at 400 turns per second.8

Foucault’s Problems

One of the problems inherent in the method as mentioned above was diffraction.  The smallness of the rotating mirror accentuated this and it resulted in a returned image whose sharpness was impaired and whose contours were altered.  To overcome this problem, Foucault used at the light source a grid of ten equal and parallel lines to the millimeter.  The resultant image thus was composed of a series of lines of maximum and minimum intensity.  The distance apart of the maxima would be the same as that of the lines of light in the grid itself, and so also for the minima.

The second problem in the technique that Foucault addressed was that the intensity of the returned image dropped off as the cube of the distance that the mirrors are apart.  In terms of Figure III, the critical distance is RM.  If that distance is too large, the returned image is too faint.  He overcame this problem by a chain of five mirrors, although initially he suggested a series of convex lenses.5a  This allowed him to have a folded light path of 20 meters within the confines of a room.  It appears that Michelson failed to appreciate this light-saving technique.9

Later experimenters overcame these problems in another way that allowed for a much longer light-path and a vastly increased distance EE’ between images.  In Michelson’s work, the lens, L, was of much longer focal length and such that R and M were virtually conjugate foci of L.2b  The source, S, was placed close to R, and with L of appropriate focus, the concave mirror, M, could be placed several miles away.  When viewed through the micrometer eyepiece, there is the direct reflection from the revolving mirror and beside it the returned image at a distance dependant upon the rotation rate.  For Foucault’s arrangement, the mirror reflected the light back to the eyepiece once every revolution, giving a flickering effect until a high enough rotation rate was achieved.10  Newcomb and Michelson used mirrors of four or more reflecting faces which also gave a brighter image.

Foucault’s Micrometer and c value

Measurement of the distance EE’ by micrometer is the vital part in the whole exercise.  The larger is this displacement of the two images, the smaller is going to be the relative error in measurement and the more accurate the value of c.  Obviously, with a larger distance for RM, the greater also will be the displacement EE’.  It is at this point that Foucault’s measurement problems began.  The short base-line of 20 meters allowed only a small displacement EE’ with the rate at which the mirror could reliably rotate.  To get the optimum displacement he took the rotation rate to 500 turns per second rather than, as outlined above, the more desirable 400.  This fixed rotation rate appears to have been used for all experiments.7a

Foucault initially determined the displacement EE’ by means of  the screw of the micrometer eyepiece.  The calibration of the micrometer was performed by measurements from it of ten spaces of the grid on the light source.  This grid had been accurately made with great care by Froment and served as the length standard for the micrometer, having ten spaces of the grid to the millimeter.  However, Foucault discovered that the screw was not as good as he had expected, and discarded this method of using it.11  Instead he fixed the micrometer at a setting of seven divisions of the grid or 0.7mm., and adjusted the distance of the mirror axis of R from the source S (Figure III) to get that exact displacement.  The distant SR was about one meter.  In a sample set of twenty measurements, the distance variation in SR was 5 mm, with the micrometer fixed at 0.7 mm, and the mirror rotated at 500 turns per second.12

However, there are some further difficulties in using the micrometer in this fashion.  We can only assume by what method the micrometer was set, as no record was left of this.  In the best case, with the mirror at rest, setting on the seventh division from the center of the grid may involve some uncertainty.  This arises from uncertainty in the accuracy of the original marking of the grid lines and from the breadth of the images from the grid, particularly under brilliant illumination.

Be that as it may, a more important problem arises since it was admitted that the returned image was altered in contour by the very effects of diffraction that he was trying to avoid.  Dorsey points out that the position of the displaced lines of maximum and minimum intensity were themselves probably changed by this effect with respect to their true position if the contours had not been altered.12a   In other words, with the mirror rotating, the position of the image of the center of the grid was systematically changed by diffraction so that the 0.7 mm was not its true displacement after all.  All Foucault’s c values would be systematically affected as a result of these micrometer/diffraction problems which give a large relative error due to the small value of the displacement.

Foucault worked on his c observations from May 22 until September 21 of 1862, and quotes his final value in references 6 and 7 as 298,000 ± 500 Km/s.13  However Harkness states that the final result from 80 observations made on September 16, 18 and 21 of 1862 is 298,574 ± 204 Km/s.14  As these seem to be the observations used by Foucault in his calculations, it is not immediately apparent how Harkness obtained his result.  These values almost certainly result from the micrometer/diffraction problem mentioned above.  This pioneer experiment could have been built on by the French, but it seems that the influence of Fizeau and Cornu concentrated attention on the toothed wheel method, as evidenced by the Perrotin series.  This left the way open for others to take up the possibilities of the method.

Enter the Americans

These possibilities were taken up by two Americans independently, Michelson and Newcomb, in that order.  Simon Newcomb (1835 – 1909) was a distinguished astronomer who was associated with both the United States Naval Observatory and John Hopkins University.  Among many other feats, he formulated a precise theoretical expression for the changing tilt of the earth’s axis by taking into account the effects of the pull of the sun, moon and planets on the earth’s equatorial bulge.  It is still known today as ‘Newcomb’s Formula.’  (However, more recent investigations by the late government astronomer from South Australia, George Dodwell, indicate an important observational anomaly in that formula which deserves further attention).15

Newcomb’s extensive report of his determinations of c during 1880-1882 appeared in 1891.16  It seems that he has been considering the project since 1867.  However, it was not until March of 1879 that Congress gave him the necessary appropriation for the work.  By then Michelson had already performed preliminary experiments and was working towards a more definitive value for c.  Michelson’s results were published in 1878 and 1880 respectively.  He had performed his experiments at the Naval Academy, Annapolis, where he was an instructor, and submitted his results to the Secretary of the Navy.  As the protocol required, the Naval Secretary forwarded the manuscript to the Nautical Almanac Office, whose Superintendent was none other than Newcomb.17

Newcomb thereupon requested that Michelson be seconded to assist him with his determination.  The required assistance was rendered during a portion of Newcomb’s first series, until September 13, 1880.  By then, Michelson had accepted an appointment to the Case Institute and moved to Cleveland, Ohio, terminating his association with Newcomb.  However, Newcomb encouraged Michelson to make an entirely new determination of c there at Cleveland, which was done in 1882, and wrote the introductory note to Michelson’s report in 1891.  Michelson continued with a more extensive series of determinations of c which will be considered after Newcomb’s set.

Newcomb’s Experiments

Newcomb utilized a square steel prism as his rotating mirror, which was 85 mm. long and 37.5 m. square.  All four faces were nickel-plated and polished.  The prism was rotated about its long axis inside a metal housing that had two open windows opposite each other.  Rotation of the prism was effected by a stream of air directed through the windows against the 12 vanes in each of the two fan wheels rigidly attached to either end of the prism.  It seems from Newcomb’s Figure 5 of Plate VI that four of the vanes were pointing in the direction of the corners of the prism on the lower wheel.  However, the prism corners were midway between vanes for the upper wheel.  Dorsey suggested that wheels of 13 vanes may have been better for symmetry and to overcome any potential problems caused by its absence.18

A stiff frame carrying the observing telescope swung about an axis coincident with that of the rotating prism.  At its other end were a pair of microscopes for reading the deflection.  The radius of the arc over which it swung was 2.4 meters.  The sending telescope was placed immediately above the observing ‘scope and had as its light source an adjustable slit illuminated by sunlight reflected from the heliostat.  Light from the slit was directed to the upper half of one of the rotating prism’s faces.  Following its return from the distant concave mirror, the light beam was reflected from the lower half of the same face into the observing telescope.

In his initial work, centering about 1880.9, the base-line was 2550.95 meters from Fort Meyer to the U.S. Naval Observatory.  For this series he used mirror speeds ranging from 114 to 254 turns per second.  In his second and third series, centered in 1881.7 and 1882.7 respectively, the base was lengthened to 3721.21 meters from Fort Meyer to the Washington Monument.  The base-line was measured by the United States Coast and Geodetic Survey.  Here, mirror speeds of 176 to 268 turns per second were employed.  The mirror rotation rate was obtained from a chronograph record of every 28 turns of the mirror, the time being recorded by a rated chronometer.

Newcomb placed the observing telescope in a suitable position and adjusted the rotation rate of the prism until the returned image was just on the cross hairs.  The prism rotation rate was then held steady until a long enough chronograph record had been obtained.  The observing ‘scope was then swung equally far on the other side of the zero deflection position, and the prism rotated in the opposite direction while the necessary quantities were noted.

This method overcame the problem of getting an accurate setting on the undeflected beam due to its brilliance and the width of the slit.  Additionally, the trouble suffered by Foucault with the lack of symmetry in the diffraction pattern was eliminated.  The difficulty of Foucault’s miniscule deflection of 0.7 mm was well under control.  The first series with the shortest base line gave double angles ranging from 10,500 arc seconds to 22,300” with an average of 15,000”.  That is an average of 4.2 which translates into about 17.5 cm for the linear deflection, the range being roughly 12 cm to 26 cm for the double angle.  This average is just 125 times the linear deflection of Foucault’s pioneer result if the single angle is taken.

Newcomb’s Problems

All told, there were three distinct series of experiments.  Michelson assisted Newcomb for part of the first series from June 28 until September 13, 1880.  The series continued until April 15, 1881, by which time 150 experiments had been performed.  Of these, Michelson had been involved with 99.  The second series went from August 8, 1881, until September 24, with 39 experiments performed.  The third series, in which Newcomb was assisted by Holcombe, extended from July 24, 1882, to September 5 of that year for a total of 66 experiments.  This made a grand total of 255 experiments.

However, they were not all equally successful.  The first series over the short path from Fort Meyer to the Naval Observatory seemed to go smoothly, but all was not as it seemed.  The second series over the longer path from Fort Meyer to the Washington Monument showed up the problem.  Newcomb had the pivots of the mirror examined and re-ground by the manufacturers at the beginning of each series.19  As the second series proceeded, abnormalities were noticed.  Different mirror faces appeared to give slightly different displacements of portions of the image.  By the 12th of September, 1881, there was no doubt.  The image was split into two pairs of parts.  The arrangement indicated that an axial vibration of the mirror was responsible with its period being half the time of rotation.  The vibration did not produce visible results below certain speeds.20

Newcomb sent the mirror to the maker on September 14th.  There, two troubles were discovered by the maker.  First, he reported the mirror to be sensibly out of balance, a condition that seems to have existed from the beginning, thereby affecting the first series.  The second problem was that the pivot was not perfectly round.  The problems were fixed and experimentation began again on the 19th, but by the 24th the pivot problem had reasserted itself.  The pivot by then had “cohered to its conical cap, and the mirror was sent to the makers for another thorough overhauling of its pivots.”21

At the same time, Newcomb arranged for the sending and receiving telescopes to have their positions interchangeable.  If the mirror was out of balance, or if there were torsional vibrations of the mirror in which the top was in a different position relative to the bottom, then interchanging the telescopes would change the sign of the systematic error.  The problem would thus be picked up and estimated, or eliminated.  Newcomb suspected that such torsional vibrations may have been present due to a static twist from the offset vanes in the fan wheels, as well as the mirror imbalance already noted.  This allowed both problems to be corrected.  However, after analysis, Dorsey decided that the magnitude of the force needed for such a static twist, whether from fan wheels or any other cause, was too high.  Furthermore, in the third series that was conducted in 1882, the reversal procedure produced a difference “too small for taking account of.”22

Thus, the third series ran smoothly, with no mirror imbalance and no upsetting vibrations detected.  The first series appeared to be affected by the presence of the vibration from the mirror imbalance.  It could not have been detected without the telescope reversals unless its period happened to be some high multiple of the time for quarter of a revolution.  This was only attained in some of the observations of series 2.  Newcomb therefore based his value of c soley on the results of series 3.  He stated, “The preceding investigations and discussions seem to show that our results should depend entirely on the measures of 1882.”23

Newcomb’s Results

The result from Newcomb’s first series of 150 experiments centering on 1880.9 over the 2550.95 meter path was 299,627 Km/s.  That from the second series of 39 experiments over the 3721.21 meters for a mean date of 1881.7 was 299,694 Km/s.  Both of these values are for air.  Newcomb did not even bother to reduce them to a vacuum or even mention their probable errors because of the problems associated with these two series.  The result from the third series of 66 experiments over 3721.21 meters with a mean date of 1882.7 was 299,860 ± 30 Km/s for a vacuum.  This was the result he favored.23a  However, with some reluctance, and only in order to avoid criticism, he included the first two series in a mean value with the third as 299,810 Km/s for a vacuum.23b  No probable error was given for this mean because of Newcomb’s dissatisfaction with it.

The Beginnings with Michelson

Albert A. Michelson was an American physicist born in 1852.  Prior to his death in 1931, he had been Professor of Physics at the University of Chicago where many famous experiments on the interference of light were done.  He had been an instructor in physics and chemistry at the U.S. Naval Academy after he had graduated in 1873.  His Superintendent questioned his “useless experiments” on light that were done while he was there.  He continued his light velocity experiments during his ten years at the Case Institute of Technology, and his work was rewarded in 1907 with the Nobel Prize.24

Michelson’s first two determinations of c were performed entirely independently of Newcomb and were personally initiated by him and privately funded.  His initial aim in the first series in 1878 was to prove that a much larger displacement was possible than Foucault obtained with his apparatus.25  His base line was 500 feet, or 152.4 meters.  The rotating mirror was thirty feet from the slit and eyepiece and achieved 130 turns per second.  Given the final result, it appears that the displacement was about ten times greater than Foucault’s, being around 7.58 mm.  Michelson had achieved his initial purpose in showing that the procedure worked.

Because of his funding situation, Michelson’s equipment was simple for the first series.  The circular mirror was silvered on one side and about one inch in diameter.  The drive comprised a blast of air that was directed against the mirror itself.  The rotation rate was measured stroboscopically.  This initial apparatus was used to obtain ten measurements of c for 1878.0, the result being 186,500 ± 300 miles/s or 300,140 ± 480 Km/s.  Note that de Bray retains the probable error of ±300 miles/s as ± 300 Km/s (no conversion) and gives the base line the same as the second series.13a

Dorsey refers to this result as “merely an exploratory determination”,26 while Michelson himself discarded it owing to its large probable error.  Michelson’s 1880 paper dealing with both this exploratory determination and the second, more sophisticated series, commented on the limitations of the initial equipment.  Referring to the mirror drive, he states “This crude piece of apparatus is now supplanted by a turbine wheel which insures a steadier and more uniform motion.”27  All told, then, this initial series is not held to be definitive by anyone.

Michelson’s New Apparatus

By mid-1878, Michelson had received a contribution of $2000 from Mr. A.G. Hemingway of New York, to be used towards another determination of c.27a   This allowed new instruments to be constructed during the remainder of that year and into the first half of 1879.  A much longer path was envisaged.  As it eventuated, the path was 1986.23 feet between mirrors, or 605.40 meters, at the U.S. Naval Academy.28  A new mirror was made of a disk of glass 1.25 inches in diameter, 0.2 inches thick, and silvered on one side only.  It was mounted in a metal ring that was part of a spinning axle having six outlets exhausting air as a form of air turbine with constant thrust.  This system overcame any erratic motion arising from Newcomb’s type of drive.  However, the disadvantage was that it could not rotate in both directions.

The mirror speed was stroboscopically determined by an electrically driven tuning fork compared with a freely vibrating standard Koenig fork on a resonator.  Comparison was made via the beat phenomenon.  The arrangement was carefully studied by Professor A. M. Mayer of Stevens Institute, Hoboken, on July 4, 1879, after the series was completed on the 2nd of July.  Two series of measurements were made averaging 256.072 and 256.068 vibrations per second at 18.3 degrees centigrade.  Originally, the fork was armed with a tip of copper foil which was lost and a platinum one of 4.6 mgm used as its replacement.  The copper tip seems to have given 256.180 vibrations per second.  All work prior to the platinum tip replacement on June 4th, 1879, was discarded.29  This comprised 30 sets of observations while the equipment was being set up and adjusted from April 2nd until June 5th.  In the actual series itself, from June 5th, the electric fork was compared by beats with the standard two or three times before every set of observations and the temperature read concurrently.

The speed of the mirror was usually 257.3 turns per second, but four sets of experiments were made on July 2nd at speeds of about 193, 128.6, 96.5, and 64.3 turns per second.  This test indicated no untoward effects or systematic errors.  However, Dorsey points out that they are harmonics of one-eighth the usual speed and any error in that harmonic could not be found.30

Because Michelson used a single lens of 45.7 meters focal length between the two mirrors instead of two telescopes, the mirror rotation axis had to be very slightly inclined to the vertical to avoid the mirror flashing light into the eyes of the observer.  The effect of this change in azimuth was tested by Michelson to see if there was any variation in speed in the mirror on that account.  His testing procedure was designed to pick up any variation due to the frame holding the mirror, friction from the pivots, or the sockets.  The azimuth angle was varied both ways and the mirror was inverted on its bearings.  These tests were carried out on June 7 and 9 for the frame inclined at various angles (ten sets of experiments), an June 30 and July 1 for the mirror inversion (8 sets).  He reported “The results were unchanged, showing that any such variation was too small to affect the result.”31

It was only possible to conduct experiments for an hour after sunrise and an hour before sunset, as an electric lamp illumination of the source slit was found unsuitable after the first experimental set, and so the sun had to be employed.  The source slit was firmly clamped to the frame of the micrometer screw that moved the eyepiece.  The distance from the micrometer and source slit to the rotating mirror was either of two values: 8.60 or 10.15 meters.  The average displacement from each was about 112.6 or 133.2 mm respectively.

The micrometer screw calibration was checked by the aforementioned Professor Mayer.  Each ‘set’ of observations consisted of the mean of ten consecutive settings of the micrometer, along with other relevant values.  Michelson invited other observers to make the micrometer readings on a number of occasions.  There were three sets on both of the evenings of June 14th and 17th made by other observers.  Their values were in close agreement with Michelson’s final mean of all observations.  The test indicates a lack of bias in the micrometer settings.

Michelson’s Second Series Results

In setting up and testing his apparatus from April 2 to June 5 of 1879, Michelson made 30 observations which were not considered in his final analysis and were not even recorded in any of his reports.  His series proper began on June 5, and concluded on July 2 that same year, and comprised precisely 100 sets of experiments.  Each set consisted of a group of ten readings as mentioned above.

Initially, Michelson gave his result as 299,944 ± 51 Km/s and then rounded to 299,940 ± 50 Km/s.31a  This value was then revised for both a false temperature correction and a trigonometrical misinterpretation of the micrometer readings.  When this was done, the final corrected value for c was given as 299,910 ± 50 Km/s for a vacuum.32  Dorsey felt that a value of 299,900 might be justifiable.33

When Newcomb mentioned the correction, he misquoted the value as 299,942 Km/s.34  Todd’s discussion refers to this value as given in the ‘corrected slip’ but quotes 299,930 Km/s.35  Some of this confusion may be traced to Michelson’s report to the American Association for the Advancement of Science.36 The report itself was published accurately.  However, an Abstract of Michelson’s report was then circulated.  The Table of values that appeared in the Abstract, and those in the ‘corrected slip’ associated with the Abstract were erroneous.37  Todd’s discussion was based on these incorrect values and so is of little worth.

Michelson’s Third Series

After moving to the Case Institute, Michelson was prompted by Newcomb to continue his investigation into the value of c.  This was carried out in 1882, essentially concurrent with Newcomb’s final series.  Michelson used virtually the same equipment as that in his second series.38  The same micrometer, the same rotating mirror, lens, and air drive were used both times.  The general optical arrangements were the same.  The main differences were the path length of 624.546 meters (the old one was 605.4 meters) and the distant fixed mirror was slightly concave and fifteen inches in diameter compared with seven inches for the old.  The same tape was used for measuring as was the previous calibration of the micrometer screw.  The new cross-checks and comparisons indicated that all was satisfactory, even for Dorsey.

The other main difference was the stroboscopic speed measurement.  The electrically driven fork made 128 vibrations per second (the old was 256), and compared by beats with the freely vibrating standard.  A clock comparison was made with the standard.  It was thus determined that the standard had 128 vibrations per second from 71 degrees F down to a low of 54 degrees F.  Everything else was the same as the previous series.  Dorsey admits that “One would expect the result to be essentially the same for each.”38a  Accordingly, the state was set for an interesting comparison of results, as this new series virtually differed only in location.

Michelson’s Third Series Results

Michelson conducted 563 experiments in his determination of c between October 12 and November 14, 1883.  The mirror was rotated at speeds ranging from 128.927 turns per second up to 258.754 with the usual speed being close to 258 turns per second.  These speeds resulted in deflections from 68.907 mm. up to 138.233 mm with the average being close to 138 mm.  The distance from the rotating mirror to the micrometer was 10.15 meters, the same as the largest separation in the second series.  Michelson’s definitive value for a vacuum in this series was 299,853 ± 60 Km/s.  As Dorsey notes, no reason is given why the probable error for this series is 10 Km/s larger than for the previous one.  Dorsey also admits that a value of 299,850 Km/s might be justifiable.  Thus, taking either the values issued by Michelson, or Dorsey’’s approximation to them, resulted in a lower value for c at the later date.

Michelson Tries Again

A few people among us do enjoy exploring new fields once they have turned 70.  Michelson was one of those.  He may have been somewhat influenced by the fact that his earlier determinations of c had been privately funded.  This time the Carnegie Institute of Washington offered to back the enterprise.  Accordingly, an improved method, a longer path and fewer financial restrictions saw Michelson rising to the challenge and conducting a new series of experiments in August of 1924, when he was 72.

The new method, which has been described as a special case of the rotating mirror experiment, actually combined features of both the old toothed wheel system and the Foucault arrangement.  It is illustrated on Figure IV.  The source of light, S, was a Sperry arc focused on a slit.  This light then passes to one face of the octagonal rotating mirror, R, and via a system of small optically flat mirrors, B and F, to the large concave mirror, D.  This sent a parallel beam of light to its twin mirror, E, some 22 miles away.  From there it was reflected by mirror G back via E to D.  From there it went into the eyes of the observer, O, by the optical flats and the opposite face of the octagonal mirror.

The system was adjusted with the octagonal mirror at rest and the image of the slit adjusted on the micrometer.  The octagon was then rotated, displacing the image.  However, at a certain critical speed, the next face of the octagon was in the position of the first face and as a consequence, the image was again undeflected.  This situation was  basically similar to the undimmed image from the toothed wheel.  This system also allowed two types of measurement.  The speed of the octagon can be measured for the undisplaced image, or, alternatively, fixing the speed at some convenient value, the image displacement can be measured by the micrometer.  Additionally, Michelson arranged for a number of rotating mirrors to be used, some of 8, 12, or 16 sides, and comparisons made.

This beautiful experiment was first suggested by Cornu,39 though Michelson did not appreciate Cornu’s view of it as harmonizing both the Foucault as well as the Fizeau methods.40  Newcomb also made the helpful suggestion that a multifaceted prismatic mirror be used in which the returned beam be reflected from the opposite face to the outgoing one.41

Details of the New Try

The twin concave mirrors each had a 30 foot focus (9.14 meters) and two foot aperture (61 centimeters).  Light was sent from Mt. Wilson Observatory in California some 22 miles to San Antonio Peak.  The measurement between the two mountain bench marks was 35,385.53 meters, with a probable error of one part in two million.42  When the distance from the markers to the mirrors is added, the final distance became 35,426.23 meters.43  The reports indicate that the glass octagonal prism was used exclusively as the rotating mirror for this determination of 1924.44  It was driven by two nozzles directing a blast of air at 40 cm mercury pressure against the six (or 8?) vanes of an open fan wheel.  Mirror speeds were about 528 turns per second and regulated by a control valve issuing a counter-blast to the fan wheel.  The distance of the micrometer from the rotating mirror was 25 centimeters and the unshifted position of the image was utilized.

The item that had to be established was the rate of mirror rotation for the unshifted position of the image.  Again, stroboscopic means were employed.  This time it was an electrically driven tuning fork of 132.25 vibrations per second.   It was compared with a free auxiliary pendulum that was itself checked against an invar gravity pendulum rated and loaned by the U.S. Coast and Geodetic Survey.  Experiments were conducted at night between August 4 and 10, 1924, and comprised ten series of observations conducted on eight occasions, giving a total of eighty experiments.

Results from the New Try

Michelson initially published a result of 2999,820 ± 30 Km/s.44a  However, it was then realized that the vacuum correction was faulty due to the altitude of the experiments and further examination of this issue resulted in a correction being issued later, giving the final value for this fourth series as 299,802 ± 30 Km/s.45  Dorsey conceded a value of 299,800 Km/s, but later points out that a further correction to the group refractive index is more appropriate than the ordinary index, and this adds another 2 Km/s to the value, leaving it as it stands.46  Because he planned to continue with further experiments using other mirrors but the same equipment, Michelson called this result ‘preliminary.’  However, the series was complete in itself and deemed of sufficient accuracy to be published at once.

Michelson’s Series Five

The arrangements for series five were virtually unchanged form the initial series four experiments.47  The main differences were occasioned by the use of a variety of mirrors.  In addition to the 8-sided glass prism used earlier, there were four new mirrors.  One was an 8-faced prism of nickel-steel which was rotated at approximately 528 revolutions per second, as the old glass octagon was.  There was a 12-faced nickel-steel mirror and a 12-faced glass mirror, the latter being 6.25 cm. in diameter, and both rotating at about 352 revolutions per second.  For the glass mirrors the drive was as before.  The steel mirrors had four air nozzles at 90 degrees that impinged upon 24 recessed buckets cut into a wheel attached to the axle.  In each case the air drive was reversible, the steel mirrors having a second bucket wheel for the occasion.

The other improvement was the use of a tuning fork of 528 vibrations per second that was driven by a vacuum-tube circuit.  This was compared directly with the same standard C.G.S. invar gravity pendulum used before.  Comparisons were made between this standard pendulum and the observatory clock on July 1 and August 15 of 1926, the agreement being to about 1 part in 100,000.  Thus, with basically the same equipment, the scene was again set for an interesting comparison of the values obtained for c.

Results from Series Five

Michelson states that “the definitive measurements were begun in June 1926 and continued until the middle of September.”47a  This is just two years after the first run with the equipment.  The mean date is 1926.5 for reasons seen shortly.  An interesting result emerged after usual appropriate weighting of the values from the five separate prismatic mirrors.  If the correct reduction to the vacuum is applies to them, they read as follows:

Glass octagon – 299.799 Km/s
Steel octagon – 299.797 Km/s
12-faced glass prism – 299,798 Km/s
12-faced steel prism – 299,798 Km/s
16-faced glass prism – 299,798 Km/s 47b

In other words, they are in agreement to within ± 1 Km/s.  It should be pointed out, however, that in the case of the glass octagon the values obtained earlier from 1924 and 1925 were lumped up with the 1926 results to get the final quote.  All told, the final result came from eight values of c, each comprising around 200 individual experiments.  The eight values derive from the above quoted five as there were two separate sets for the 16-faced glass prism and 3 separate sets for the glass octagon, including the 1924 results.  Thus, about 1600 individual experiments were performed to obtain the final value for the fifth series.

Michelson then quoted a final value of 299,796 ± 4 Km/s in his report.  However, as Birge pointed out, the final value had to be revised upwards 2 Km/s due to Michelson’s failure to take account of the group velocity correction.48  Additionally, despite the close agreement of the above results, Birge felt that the variety of temperatures and pressures that would have been encountered introduced an element of uncertainty.  Consequently, he and Dorsey put the corrected value at 299,798 ± 15 Km/s.  Michelson’s statements in Studies in Optics (1927: 136-137) and those in Encyclopedia Britannica (23:34-38, 1929) give misleading impressions about the values obtained from this series and should be ignored.

Following this series, Michelson endeavored to try with the same equipment a series of experiments over a path from Mt. Wilson Observatory to Mt. San Jacinto, a distance of about 82 miles, or roughly 131 Km.  However, because of bad atmospheric conditions, the experiments were abandon and the initial results obtained were not considered reliable enough for publication.49

With essentially the same equipment, therefore, Michelson obtained 299,802 Km/s for his results in 1925.6, and 299,798 Km/s for his results in 1926.5.  This was the second time that two series by Michelson have shown a lower value for c on the second occasion with the same equipment.  However, that is not all.  Comparison between those two sets of series also shows a drop with time.  In other words, four determinations, in two sets of two, show a consistent drop with time through the four, within each of the two related sets, and between the two sets.  As noted previously, Michelson’s results alone indicate, on a least squares analysis, a decay of 1.86 Km/s per year over the 47 years of his c experimentation.  These last two series suggest about 2 Km/s per year for the decay rate.

Dorsey’s Comments

Dorsey noted for Michelson’s work that “Although each series of determinations has yielded a value that differs from each of the others, Michelson has made no attempt in his reports, or elsewhere, so far as I know, to account for these differences.”50  This statement still holds even if Dorsey’s modified values for Michelson’s work are used.  With a persistent drop in values for c by a single experimenter, as well as for all values by any particular method, one would imagine that the simplest explanation that Michelson or Dorsey could offer is that the physical quantity itself is dropping with time.  De Brey suggested this, but Dorsey preferred to have his problem unsolved rather than accept that explanation.

Indeed, Dorsey tried to overcome the problem by invoking the action of vibrations.  However, this was tested for each time.  The single mirrors were able to be inverted or have their azimuth changed to cross-check that possibility while the multi-faceted mirrors could be rotated both ways to check.  No vibrations were discovered by these processes.  Dorsey suggested, however, that this meant vibrations were at a maximum!  It is an argument from silence as no evidence of such anomalous motion was discovered, whether it be blurred, split, or multiple images or asymmetric broadening such as Newcomb found with his work which genuinely did have vibration troubles.

On the basis of this evidence from silence, Dorsey then claims that all series had vibrations that would give rise to the lower value for c in the 1924-26 determinations compared with the 1878-80 series.  He does not elucidate why a drop in c would result from vibrations being present in BOTH cases.  Furthermore, he ignores the small drop in c that was picked up within both the 1878-80 series and the 1924-26 determinations.  Indeed, since the same equipment was being used, Dorsey’s proposed vibrations would be equally present within the 1879-80 series or the 1924-26 series, and all measurements then equally affected.  The drop in c within each of the series is not the result of this proposed systematic error, then, but despite it.  It would be picked up whether or not the systematic error was there.  All any systematic error (real or imaginary) does is to shift the effect into another range of values, and Newcomb’s experience suggests that Dorsey’s proposed vibrations would give a measured value of c below its true value.  Accordingly, as all Michelson’s results are above the present value of c, and vibrations would seem to lower the result, then all these values should be corrected upwards if Dorsey’s vibration idea is accepted, thus accentuating the already observed trend.

Michelson’s Last Experiment

Because of the increasing accuracy and necessity for precise vacuum correction, Michelson decided tin 1929 to initiate what was to be his last final experiment.  His collaborators were Pease and Pearson.51  The idea was that a one mile long pipe would be exhausted of its air and by repeated reflections from mirrors at either end a path length of some ten miles could be achieved in a fair vacuum.  Pressure in the pipe varied from 0.5 to 5.5 millimeters of mercury.  The arrangement was essentially that shown in Figure V.  A carbon arc source was at S focused on an adjustable slit 0.075 mm wide and was reflected from a 32-faced rotating mirror, R.  The mirror was a glass prism 0.25 inches long and 1.5 inches along the diagonals of its cross-section.  All its angles were correct to one arc second and its surfaces to 0.1 wave.

Light was reflected from the upper half of face ‘a’ of the mirror through a glass window, W, that was 2 cm. thick, into the pipe and via the mirrors Q and N, onto the large optically flat mirrors M and p, 55.9 cm. in diameter.  N was essentially a concave mirror 101.6 cm in diameter and of 15.02 m. focus that gave a parallel beam forming and image of the slit on M.  After repeated reflections from M and P, the beam was returned through the window to strike the lower half of face ‘b’ of the rotating mirror, if it were at rest, and into the eye of the observer E.  The distance from the rotating mirror to the eyepiece micrometer was 30 cm.  In operation, the mirror was rotated at such a speed that face ‘a’ would move into the position occupied by face ‘b’ in the time that the light took to be reflected along the pipe and return.  Depending on the adjustment of the four fixed mirrors, light could travel eight or ten miles before being returned to R.

The two distances required different rotation rates of the prism.  For a distance of 7,999.87 meters, the rotation rate was about 585 revolutions per second, while 6,405.59 meters required about 730 revolutions per second.  This rotation rate was again controlled and determined stroboscopically with a tuning fork compared with a free pendulum swinging in a heavy bronze box of constant temperature and low pressure.  The pendulum was itself compared with a time-piece that was checked against time signals from Arlington, Virginia.

In practice, the speed of the mirror was held at some convenient value close to the position where the returned beam was undeflected.  The difference from the precise 1/32 of a revolution was determined by measuring the deflection with the micrometer.  The mirror was, in fact, reversed at the same convenient speed and the double displacement measured.  The drive was a compressed air turbine.  Also capable of reversal we the arrangement whereby light from the slit hit the top of face ‘a’ while the returned hit the bottom of face ‘b’.  In this it was similar to Newcomb’s arrangement to check for any vibrational errors.  Correction for residual air in the pipe was done for each experiment.

Over to Pease and Pearson

Michelson made preparation for this c determination from 1929 until February 19, 1931, when the experiments actually began.  The work was sponsored by the University of Chicago, the Mount Wilson Observatory, the Carnegie Corporation and the Rockefeller Foundation.  The evacuated pipe was constructed of Armco-iron steel sheets and was one meter in diameter.  It was situated by Laguna Beach, in California, on the Irvine Ranch close to Santa Ana.  Michelson began his measurements on February 19, 1931, when he was 79, and was ably assisted by Pease and Pearson.  The work continued on until February 27, 1933, with a total of 233 series of observations comprising 1110 sets, making 2885 experiments all told for the full determination.  However, after spending a lifetime measuring c and studying the behavior and properties of light, Michelson died on May 9, 1931, after completing only 36 of the 233 series. 

Even while they were working, Pease and Pearson noticed a peculiar circumstance.  Irregular as well as regular variations in the value of c obtained occurred hourly and daily, as well as over longer periods – up to a year.  Deviations of 10 Km/s over a period of a week or so were common, and occasionally they went as high as 30 Km/s.52  Within the 233 series conducted, the average deviation from the mean value of a series is about 10.5 Km/s.  As Cohen points out, “The base line was on very unstable alluvial soil.  A correlation between fluctuations in the results and the tides on the sea coast was reported.”53  For good measure, the base-line was discovered to be fluctuating from other causes as well.  As Birge noted, Pease and Pearson “found their carefully measured mile-long base line showed for two years a steady increase in  length of 6.5 mm. per year…and then a sudden decrease of 8mm after a mild earthquake in the vicinity.”54  As the base line was only measured on those three occasions, one wonders what else it was doing in the meantime, being not only by the sea coast, but also right by the main fault line, as well as considering the fact that the pipe was joined by many seals.

Dorsey notes something else that may be relevant.  Though he continues on about possible vibrations that Pease and Pearson established as negligible, he points out that the micrometer only read directly to 0.001 inches.55  This corresponds to a velocity of 32 Km/s.  Yet this was used to establish the displacement from the central position and the mean deviation of the sample five readings from their mean is about 0.00025 inches.

It is for these reasons that Pease and Pearson’s final quoted value of 299,744 ± 10 Km/s is regarded today as unacceptably low due to systematic errors in the micrometer readings and problems with an unstable base line.  The plot of distribution frequency of all 2885 values compared with the mean value is enlightening.  There were 1095 values that lay in the range of 299,770 to 299,780 Km/s and 1790 values outside it.  Of this latter number, 1025 values were below 299,770 and only 765 above 299,780.  The distribution is plainly unsymmetrical and thus differs appreciably from the normal error curve, there being an excess of low values.

Conclusions From Rotating Mirrors

The results of the rotating mirror experiments are summarized in Table 6.  If the results rejected by the experimenters themselves are omitted along with Fourcault’s admittedly pioneer experiment which was “intended to ascertain the possibilities of the method,”13b then a least squares linear fit to the six data points gives a decay of 1.85 Km/s per year.  The value of the correlation coefficient, r, equals -0.932, with a confidence interval of 99.6% in this decay correlation.  Omitting Pease and Pearson’s result gives a decay of 1.74 Km/s per year, with r = 0.905, this correlation being significant at the 98.2% level.  There is also a 95.6% confidence interval that c was not constant at its present value during the years of these experiments.

Table 6
Rotating Mirror Experiments
(NOED = number of experiments done)

Comments

1. Foucault:  Micrometer and diffraction problems coupled with miniscule deflection.

2. Michelson:  Value discarded by Michelson – large probable error and crude equipment.

3. Michelson:  Number of experiments listed as 100, but there were ten sets per experiment.

4. Newcomb:  This mean resulted from the inclusion of two series whose results Newcomb rejected as unreliable due to systematic errors (mirror imbalance and vibration).  These results were 299,627 Km/s in 1880.9 and 299,694 Km/s in 1881.7, both for air.  They were included with the final reliable value to get a vacuum mean only in order to avoid criticism.  These figures give the average displacement and range of rotation rates and the total number of experiments conducted.  The smaller path is quoted.

5. Newcomb:  Definitive value.  He insisted that his results “should depend entirely on the measures of 1882.”

6. Michelson:  This 1882.8 result was obtained with the same equipment as his 1879.5 result.  This value is lower.

7. Michelson:  Essentially a new method.  An octagonal glass prism with a rotation rate giving no deflection.

8. Michelson:  Polygonal mirrors of 8, 12, and 16 faces.  Result corrected for group velocity.  Equipment the same as for 1924.6.  This new method registered a decay in c over two years approximately equal to 2 Km/s per year.

9. Pease/Pearson:  Unstable baseline and minute deflection giving micrometer problems.  Generally disregarded today.

References: