Zero Point Energy, Light and Time

Barry J. Setterfield

published in the proceedings of the Natural Philosophy Allliance, vol 9, 2012

Abstract: In 1911, Planck’s equations indicated the presence of an energy-intrinsic to the vacuum of space. Called the Zero Point Energy (ZPE), it was discovered to control the properties of the vacuum, including the electric permittivity and magnetic permeability. The ZPE consists of electromagnetic waves of all wavelengths. The initial purpose of this study was to explore the effects of a varying ZPE on atoms and atomic constants, such as Planck’s constant, h, the speed of light, c , and the rest masses of atomic particles, m. The rate of ticking of atomic clocks, including radiometric clocks, can also be shown to be affected, whereas orbital clocks (gravity-based) are not. The ZPE has been shown by Haisch, Puthoff and others to maintain atomic orbits throughout the cosmos. Therefore, an increasing ZPE may mean more energetic orbits, resulting in bluer emitted light through time. This gives an alternate explanation to the increasing red shifts which are seen in progressively more distant galaxies. Alteration of electric and magnetic properties of the vacuum would also affect the speed of plasma interactions. Since the universe is usually considered to have begun as plasma, the rates of galaxy, star and planet formation using plasma physics can be shown to have been more rapid than models based on gravity. This may resolve some astronomical anomalies at the frontiers of the universe. An increasing ZPE also has implications for planetary geology, as well as giving a reason for gigantism in Earth’s fossil record. Finally, many of relativity’s predictions follow logically from the presence of a real ZPE and can be formulated with simple mathematics and intuitive concepts.

Exploring the Vacuum
Concepts of the Vacuum
Evidence for the Existence of the ZPE
ZPE Waves and Particle Pairs
Introducing the Speed of Light

Behavior of the ZPE
Dynamics of the Universe
Cosmic Expansion and Planck Scale Effects
The Origin of the Zero Point Energy
Implications for Quantum Physics

The ZPE, Planck’s Constant, and Light Speed
The ZPE and Planck’s Constant, h
The Invariance of hc
Measured Variation in the Speed of Light, c

The ZPE, Atomic Masses and Atomic Time
The ZPE Origin for Atomic Mass
Atomic Frequencies and Atomic Clocks

The ZPE and the Redshift
The ZPE and Atomic Orbits
The Behavior of the ZPE Through Time

Implications in Other Disciplines
Implications for Plasma Physics
Support from the Fossil Record

The ZPE and Relativity
The Concept of the “Ether”
Increasing Masses and Slowing Clocks
Bending Light in a Gravitational Field
Is There an Absolute Reference Frame?
Gravity, General Relativity and the ZPE

Conclusion

References

 

Exploring the Vacuum

Concepts of the Vacuum

During the 20th century, our knowledge regarding space and the properties of the vacuum took a considerable leap forward. The vacuum of space is popularly considered to be a void, an emptiness, or just ‘nothingness.’ This is the definition of a so-called bare vacuum. However, as science has learned more about the properties of space, a new and contrasting description has arisen, which physicists call the physical vacuum.

To understand the difference between these two definitions, imagine you have a perfectly sealed container. First remove all solids, liquids, and gases from it so no atoms or molecules remain. There is now a vacuum in the container. This gave rise to the 17th century definition of a vacuum as a totally empty volume of space. Late in the 19th century, it was realized that the vacuum could still contain heat or thermal radiation. If we insulate our container with the vacuum so no heat can get in or out, and if it is cooled to absolute zero, or about -273 degrees C, all thermal radiation has been removed. It might be expected that a complete vacuum now exists within the container. However, both theory and experiment show this vacuum still contains measurable energy. This energy is called the Zero-Point Energy (ZPE) as it exists even at absolute zero.

The existence of the ZPE was not suspected until the work of Max Planck in 1911, backed up by investigations by Einstein and Stern in 1913, and Nernst in 1916 [1, 2, 3].  The ZPE was discovered to be a universal phenomenon, uniform, all-pervasive, and penetrating every atomic structure throughout the cosmos. It is composed of electromagnetic waves of all wavelengths down to about 10-35 meters, at which length the waves are simply absorbed into the structure of the vacuum. We are unaware of its presence for the same reason that we are unaware of the atmospheric pressure of 14 pounds per square inch that is imposed upon our bodies. There is a perfect balance within us and without. Similarly, the radiation pressures of the ZPE are everywhere balanced in our bodies and measuring devices.

Evidence for the Existence of the ZPE

Because the ZPE is composed of many more waves of short wavelengths than long (it has a frequency cubed spectrum), the fluctuations of the ZPE waves do not become significant enough to be observed until the atomic level is attained. This explains why cooling alone will never freeze liquid helium. Unless pressure is applied, ZPE fluctuations prevent helium’s atoms from getting close enough to permit solidification.

In electronic circuits, such as microwave receivers, another problem arises because ZPE fluctuations cause a random ‘noise’ that places limits on the level to which signals can be amplified. This ‘noise’ can never be removed no matter how perfect the technology.

Further evidence comes from what is called the Lamb shift of spectral lines. The ZPE waves slightly perturb an electron in an atom so that, when electrons make a transition from one state to another, the atom emits light whose wavelength is shifted slightly from the position that line would have had if the ZPE did not exist.

The Casimir effect also indicates the existence of the ZPE in the form of electromagnetic waves.  This effect can be demonstrated by bringing two large metal plates very close together in a vacuum. When they are close, but not touching, there is a small but measurable force that pushes them together. The explanation of this effect comes straight from classical physics. As the metal plates are brought closer, they exclude all wavelengths of the ZPE except those which fit exactly between the plates. In other words, all the long wavelengths of the ZPE have been excluded and are now acting on the plates from the outside with no long waves acting from within to balance the pressure. The combined radiation pressure of these external waves then forces the plates together. In November 1998, Mohideen and Roy reported verification of the effect to within 1% [4].

ZPE Waves and Particle Pairs

Since ZPE waves go in all directions, they impact each other in somewhat the same way as waves in the ocean. Where ocean waves meet, due to a boat passing or strong cross-currents, they crest and form whitecaps which then die down quickly.  When ZPE waves meet, something similar happens: they create a concentration of energy that results in the formation of a positive and negative pair of particles, like a positive and negative electron, or a positive and negative proton, or a positive and negative pion. These particle pairs flash into existence momentarily, then re-combine and annihilate. For this reason they are referred to as virtual particles. It has been estimated that today, at any given instant, there are about 10⁶³ virtual particles flashing into and out of existence in the volume of any cubic meter. SED physics, the branch of physics which accepts the ZPE as a real entity and not just a mathematical abstraction, predicts that there is a veritable zoo of all kinds of virtual particle pairs inhabiting the vacuum.

The presence of virtual particle pairs can be demonstrated experimentally.  Take two metal plates that have leads attached to a power supply and the appropriate measuring devices.  Place a ceramic disk between the two plates.  Electricity is turned on and the voltage between the two plates is built up.  As long as the voltage continues to build, a current is shown to be flowing through the ceramic disk, between the two plates.  But when the voltage has stabilized at any particular chosen point, the current is no longer measured as flowing through the ceramic disk.  But since a current is not expected to flow through a ceramic disk at all, why was a current in evidence when the voltage was being ramped up?

As the voltage difference built up between the plates, the electric field between them affected the molecules in the ceramic disk.  Each molecule in the disk has both a positively charged and a negatively charged segment. (The exact geometrical arrangement of these charges depends on the type of molecule we are dealing with.) As the applied voltage increased, the positive end of the molecule was attracted to the negatively charged plate, while the negatively charged part of the molecule was attracted to the positively charged plate. As the voltage increased, so did the pull on the molecules, which then stretched like rubber bands. When the voltage between the plates stopped increasing, the continuing stretching ceased, and so the current stopped flowing.  Once the voltage difference is stable between the plates, the molecules have stretched to their maximum under that voltage and that is why the current is no longer flowing through the disk. The ceramic disk is then said to be polarized, because all the positive charges are aligned one way and the negative charges are aligned another.

The current in the ceramic disk caused by the motion of these molecular charges over a short distance is called a “displacement current.” The charges are simply displaced a short distance from their original positions.

If the experiment is then repeated without the ceramic disk, but in a vacuum in which all possible air is removed, it has been found that, again, a displacement current flows between the two plates. Although the displacement current is not as strong as it was using the ceramic disk, a displacement current does flow. This indicates the vacuum has electric charges which can be polarized just as the molecules in the ceramic disk were.

Polarization can only occur if there are charged particles capable of being moved or re-oriented in an electric field. The conclusion is that the vacuum must contain charged particles, capable of moving, which are not associated with the air.  This would seem to indicate the presence of virtual particle pairs. Their presence means we have a “polarizable vacuum.”  The extent to which the vacuum “permits” itself to be polarized in an electric field is called the electric permittivity of free space. This permittivity is designated by the Greek letter ε.

It is important to understand that any electric charge in motion will produce a circling magnetic field – every electric current has a circling magnetic field.  This is what gives rise to the term “electromagnetism.”  It is in this area that other experiments using magnetism have shown the ceramic disk and the vacuum share a corresponding property. In the examples above, all the charges (whether molecular or from virtual particles) were required to move in order to produce the displacement current, thus producing a magnetic field. The degree to which a magnetic field can permeate a substance is called its magnetic permeability. The presence of virtual particles causes the vacuum of space itself to have a permeability as well as a permittivity. The magnetic permeability of space is designated by the Greek letter µ.

Any changes in the strength of the Zero Point Energy would affect both the permeability and permittivity of space. If the Zero Point Energy built up with time, there would be more ZPE waves intersecting and hence more virtual particle pairs produced per unit volume. This would increase the permittivity and permeability as well.  In a similar way, if the ZPE strength decreased, so, too, would the number of virtual particles in a given volume. As a consequence, the vacuum permittivity and permeability would also decrease in direct proportion. Both ε and µ are directly proportional to the strength of the ZPE. We can write this as follows:

ε ~ µ ~ U.                                             (1)

In Eq. (1) the ZPE strength is designated by the letter U, and the symbol ~ means “is proportional to” throughout this paper.

Introducing the Speed of Light

Every photon of light must navigate the virtual particles it comes in contact with.  As a photon moves through the vacuum, it will be absorbed by virtual particles. But virtual particle pairs will recombine and annihilate extremely rapidly, releasing the photon to continue on its way. The more virtual particles a photon of light must navigate, the longer it takes to reach its final destination. Because of the extreme numbers of virtual particles, there will be huge numbers of photon/particle interactions even over very short distances.

As a result, if the strength of the ZPE changes over time, there will be a corresponding and directly proportional change in the numbers of virtual particles in a given volume of space. If the ZPE strength increases, the vacuum will become “thicker” with virtual particles. The speed of light, c, will therefore drop in inverse proportion. This is verified by the standard equation

1/(εµ)  ~  c².                                           (2)

When the results from Eq. (1) are combined with Eq. (2) then it can be seen that

c ~ 1/ε  ~  1/µ  ~ 1/U.                                  (3)

Therefore, any change in the energy density (strength) of the ZPE will produce proportional changes in the permittivity, ε, and permeability, µ, of free space and an inversely proportional change in the speed of light, c. In addition, since Planck’s equations in his 1911 paper revealed that the constant, h, which is now known as Planck’s constant, was a measure of the strength of the ZPE, its value will also change in direct proportion to the changes in ZPE strength.

Behavior of the ZPE

Dynamics of the Universe

Although it is currently thought the universe is rapidly expanding, hydrogen cloud data indicate that the universe underwent initial expansion and then became static. As light passes through the hydrogen clouds, selective wavelengths are absorbed and this produces a dark line on the spectrum. The dark line of importance here is called the Lyman Alpha line. As the light goes through an increasing number of hydrogen clouds on its journey, an increasing number of Lyman Alpha lines are built up in the spectrum. Since the clouds further away from our galaxy have greater redshifts, the position of the Lyman Alpha line on the color spectrum from an individual cloud will be dependent on distance and hence registered by its redshift. As a result of traveling great astronomical distances, light passing through these clouds will arrive at earth with a whole suite of lines. This is referred to as the 'Lyman Alpha forest.'

Analysis indicates that, if the universe is expanding, the average distance between the hydrogen clouds should be increasing as we come forward in time, and so nearer to our own galaxy. This means that as we look back into the past, and hence to greater redshifts, the clouds should get closer together. If the universe is static, the average distance apart of the clouds should remain fixed. A detailed study of this matter has been performed by Lyndon Ashmore. [5] The Abstract to one of his papers contains these conclusions:

"This paper examines the Lyman Alpha forest in order to determine the average temperature and the average separation of Hydrogen clouds over the aging of the universe. A review of the literature shows that the clouds did once become further and further apart (showing expansion?) but are now evenly spaced (an indication of a static universe?). ... Whilst these results do not support any cosmology individually, they do support one where the universe expanded in the past but that expansion has now been arrested and the universe is now static"[6].

So when did the universe stop expanding?  The data reveal that expansion occurred from the origin of the cosmos up until a time corresponding to a redshift of z = 2.6. From then down to a time corresponding to z = 1.6 the expansion ceased and the cosmos has been static from z = 1.6 down to the present. Narlikar and Arp established in 1993 that a static cosmos would be stable against collapse if it had matter in it and was undergoing slight oscillations. The model adopted here agrees with these data and concepts.

Cosmic Expansion and Planck Scale Effects

It is generally accepted that the Planck length of 10^-35 meters is the length at which the 'fabric' of the vacuum breaks down and space assumes a granular structure. The initial expansion or stretching of the fabric of space would have resulted in a tension or stress or force manifesting at the Planck scale. In other words, energy was being invested into the fabric at its most basic level. Evidence also indicates that extremely high initial temperatures were involved as expansion began.

Parallel conditions in high energy physics laboratories result in the production particle-antiparticle pairs. The process involves conversion of inherent energy into mass on the basis of E = mc². Thus the enormous tensional energy in the fabric of space that was being generated by the expansion, coupled with the extremely high temperature, would similarly have resulted in the formation of particle-antiparticle pairs. These positively and negatively charged particle pairs manifesting at the Planck scale would maintain the electrical neutrality of the vacuum.

C.H. Gibson [7] as well as Hoyle, Burbidge and Narlikar [8], have shown that processes initially operating at Planck scales would result in the formation of cascades of pairs of Planck particles. These particles have the unique property that their diameter is the same as both the Planck length and their own Compton wavelength. They are thus specifically a Planck scale phenomenon. As a result, the enormous tensional energy and extreme temperatures at the Planck scale would be expected to produce cascades of Planck particle pairs (PPP).

Gibson notes that if a Planck Particle Pair becomes misaligned as they collapse, they form a Planck-Kerr particle (P-KP). Gibson states that "a truly explosive result can occur [when] a Planck-Kerr particle forms, since one of these can trigger a big bang turbulence cascade [of Planck particle pairs]." [7] Hoyle, Burbidge and Narlikar have a different proposal which, however, has essentially the same result. [8] The same outcome is that the extreme temperatures and the enormous expansion energy provided an environment at the Planck scale in which energy was irreversibly converted to matter as a turbulent cascade of PPP and/or P-KP.

The Origin of the Zero Point Energy

Gibson, Hoyle and others have shown that, as a result of these processes, there would have been extreme turbulent vortices and separation among the PPP and P-KP. Gibson's analysis revealed that PPP and P-KP numbers would continue to increase until all turbulence had died away. He showed that such systems are characteristically inelastic, while Bizon established that inelastic systems have stronger vortices and longer persistence times [9].

Given this system, the separation of electric charges among the particle pairs would produce electric fields, while their turbulent movement would produce magnetic fields. In addition, P-KP radiate electromagnetic energy into their turbulent environment. This is the origin of the initial electro-magnetic fields of the ZPE.

After the universal expansion ceased, vortices and turbulence would persist until all the turbulent energy had been converted to PPP, as explained in detail by Gibson [7]. Because of the inelasticity and size of the system, the persistence and decay phases of turbulence may be expected to have lasted a long time. During this time the ZPE strength would continue to build because the Planck Particle Pair numbers would continue to be building.

Because PPP are both positively and negatively charged, they would continue recombining after expansion and turbulence had ceased.  Their recombination results in their annihilation, releasing their combined energy as electromagnetic radiation.

A similar process occurs when electron/positron pairs annihilate. Thus the electromagnetic fields and waves of the ZPE would continue to build up after the decay in turbulence until all PPP had recombined. Puthoff and other authors have shown that the ZPE strength is then maintained by a feedback cycle [10]. Nevertheless, an ongoing oscillation will occur in the strength of the ZPE because of the oscillation in the size of a static universe, as outlined by Narlikar and Arp in [11].

Implications for Quantum Physics

In 1962 Louis de Broglie published a book, New Perspectives in Physics [12]. In this book he pointed out that serious consideration of Planck’s second theory (1911) had been widespread until around 1930. Planck’s 1911 approach had embraced classical theory plus an intrinsic cosmological ZPE. De Broglie’s book initiated a re-examination of this approach since it showed that quantum processes actually had viable explanations in terms of classical physics, as long as the real Zero Point Energy was included.

As a result, Edward Nelson published a landmark paper in 1966. The abstract states in part:

“We shall attempt to show in this paper that the radical departure from classical physics produced by the introduction of quantum mechanics 40 years ago was unnecessary. An entirely classical derivation and interpretation of the Schrödinger equation will be given, following a line of thought which is a natural development of reasoning used in statistical mechanics and in the theory of Brownian motion” [13].

By “Brownian motion,” he was referring indirectly the effects of the ZPE.  His derivation of the Schrödinger equation using statistical mechanics gave an alternative to the esoteric view of quantum mechanics (called the Copenhagen interpretation) -- an alternative rooted in classical physics and the reality of the ZPE.

With this impetus, Boyer, in 1975, used classical physics plus the ZPE to demonstrate that the fluctuations caused by the Zero-Point Fields (ZPF) on the positions of particles are in exact agreement with quantum theory and Heisenberg’s Uncertainty Principle (HUP) [14]. In this approach, the HUP is not merely the result of theoretical quantum laws. Instead, it is due to the continual battering of sub-atomic particles, as well as the atoms themselves, by the impacting waves of the ZPE. This continual ‘jiggling’ at speeds close to the speed of light means it is virtually impossible to pinpoint both the position and momentum of a subatomic particle at any given instant in time.  Instead of merely being a theoretical concept, the ZPE provides a reason for this indeterminate position and momentum. In this way, classical physics using the ZPE, offers explanations in reality which quantum mechanics can only attempt to deal with in terms of theoretical laws.

De Broglie’s 1924 proposal that matter could behave in a wave-like manner was also examined.  These wave-like characteristics of electrons were shown to exist in 1927 by Clinton Davisson and Lester Germer [15].  De Broglie himself had supplied a basis for the ZPE explanation. He suggested that the famous equation E = mc² and Planck’s E = hf, could be equated. In these equations, ‘E’ is the energy of the particle of mass ‘m’, and ‘c’ is the speed of light. This gives a frequency, f = mc² /h , which is now called the Compton frequency. De Broglie felt that this frequency was an intrinsic oscillation of the charge of an electron or parton. If he had then identified the ZPE as the source of the oscillation, he would have been on his way to a solution.

Haisch and Rueda point out that the electron really does oscillate at the Compton frequency, when in its own rest frame, due to the ZPE. They note

“… when you view the electron from a moving frame there is a beat frequency superimposed on this oscillation due to the Doppler shift. It turns out that this beat frequency proves to be exactly the de Broglie wavelength of a moving electron. … the ZPF drives the electron to undergo some kind of oscillation at the Compton frequency… and this is where and how the de Broglie wavelength originates due to Doppler shifts.” [16]

Thus the Compton frequency is due to the ZPE-imposed oscillation of the particle at rest. The de Broglie wavelength results from both the motion of the particle and the oscillation, appearing as a "beat" phenomenon.

This approach, using classical physics plus a real ZPE, is now called Stochastic Electro-Dynamics (SED). This contrasts to the more commonly used Quantum Electro-Dynamics (QED). SED physics has been able to derive and explain the black-body spectrum, Heisenberg’s Principle, the Schrödinger equation, and the wave-nature of sub-atomic matter. These were the exact factors that, interpreted without the ZPE, gave rise to QED physics. So it is possible that physics took a wrong turn in the mid-1920’s.

The ZPE, Planck’s Constant, and Light Speed

The ZPE and Planck’s Constant, h

In his 1911 paper, Planck had demonstrated the existence of the ZPE [1].  His equation for the radiant energy density, ρ, of a black body had a temperature-dependent term, just as he had derived in his 1901 paper. However, it had an additional hf/2 term that was independent of temperature as in Eq. (4). This indicated a uniform, isotropic background radiation existed.

ρ(f,T)df = (8πf²/c³){[hf/(e^hf/kT – 1)] + [hf/2]} df                                         (4)

Here, f is radiation frequency, c is light-speed, and k is Boltzmann’s constant. If the temperature, T, in (4) drops to zero, we are still left with the Zero Point term, hf/2, in the final set of square brackets.  Since T does not occur in that final set of terms, that means they are temperature independent.  Planck’s constant, h, only appears in the Zero Point term as a scale factor to align theory with experiment; no quantum interpretation is needed. Being a scale factor means that if the ZPE strength was greater, then the value of h would be correspondingly larger. This means h turns out to be a measure of the strength of the ZPE. From (4), the energy density, U, of the ZPE is then given by multiplying hf/2 by the expression in the first set of square brackets, giving us

U(f) df = (4πhf³ /c ³) df .                                  (5)

Therefore, if the ZPE strength, U, increases, h must also increase proportionally. Thus we can write:

h  ~  U,                                               (6)

where U is the energy density of the ZPE. Experimental evidence for variations in h and h/e have been obtained as graphed in Figs. 1 and 2. It should be noted that the value of h increased systematically up to about 1970. Afterwards, the data show a flat point or a small decline.

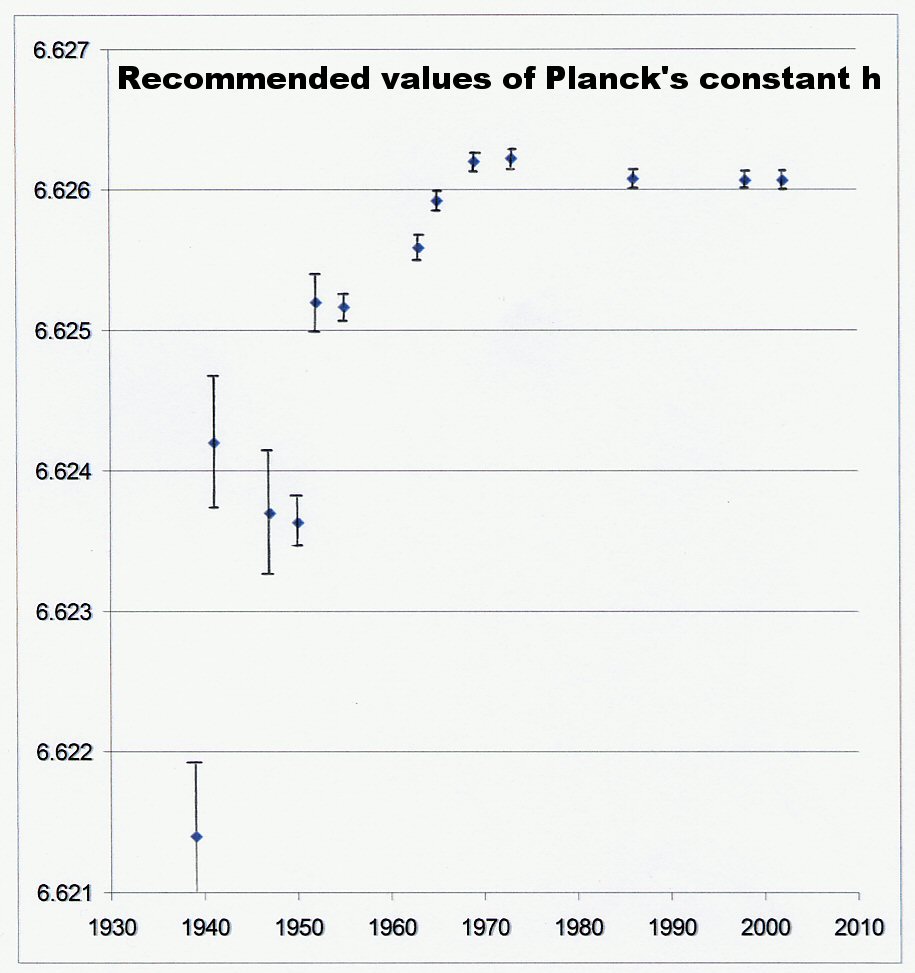
Fig. 1.  Recommended values of Planck's constant, h [17-29].

In 1965, Sanders pointed out that the then increasing values for h could only partly be accounted for by the improvements in instrumental resolution [30]. One reviewer, preferring the changes in h to be a matter of instrumental improvements, nevertheless remarked that this "may in part explain the trend in the figures, but I admit that such an explanation does not appear to be quantitatively adequate."[31]  That problem was compounded since other quantities such as e/h (where e is the electronic charge), h/2e (the magnetic flux quantum), and 2e/h (the Josephson constant), all show synchronous trends centered around 1970, although measured by different methods than those used to measure h.

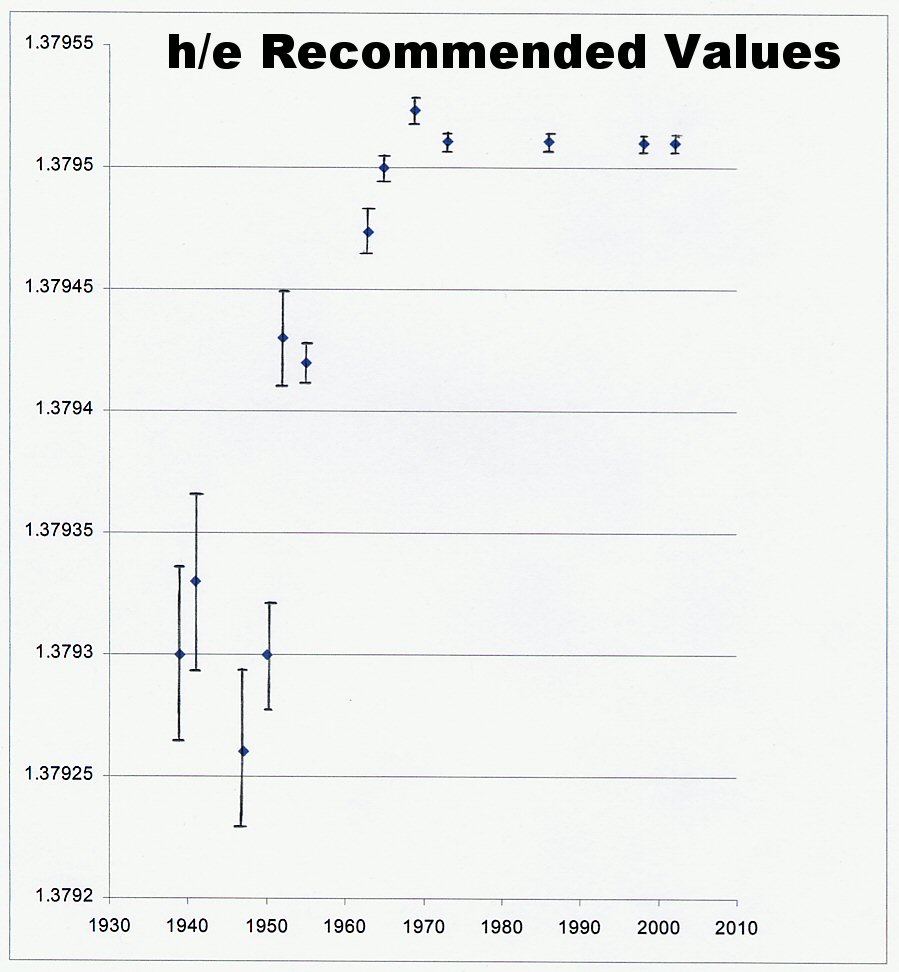
Fig. 2.  Graph of recommended values of h/e [17-29]

The Invariance of hc

A variety of data accumulated from astronomical observations out to the frontiers of the cosmos indicate that

hc = invariant, so that  c ~ 1/h .                           (7)

This conclusion is supported to an accuracy of parts per million. Some of the early experiments were performed by Bahcall and Salpeter [32], Baum and Florentin-Nielsen [33], and Solheim et al [34].  Noerdlinger [35] also obtained the early result that the quantity d[ln (hc)] / dz < 3 x 10^-4 , where z is the redshift of light from distant galaxies.

More recently, studies have focused on the fine structure constant, α[36]. This constant is a combination of four quantities such that α = [e² /ε] [1 / (2hc)], where e is the electronic charge, and ε  the vacuum permittivity. Early observations have unequivocally shown hc is cosmologically invariant as in (7). However, observational evidence has shown that α is also stable to one part in a million [37].  Given the data that leads to (7), these results also require that throughout the cosmos

e²/ε  = constant.                                       (8)

The basic constancy of (8) over astronomical time was established early on by Dyson [38], Peres [39], Bahcall and Schmidt [40] and Wesson [41].

These data, which uphold the constancy of α, are often taken as applying tight restrictions on any variability of the speed of light on a cosmological time scale. This has been the subject of John Webb’s research for a number of years [42]. There have only been very small suspected changes in the value of the fine structure constant, α.  For this reason, those holding to a minimalist position regarding the variation of atomic constants have stated that c cannot vary by any more than 1 part in about a million throughout astronomical time.  However, if the ZPE approach is adopted, it is to be expected that hc will remain fixed, but that the extent of any individual variation in h and c separately cannot be deduced from these data alone.

This means that quantities like hc, or the fine structure constant, α, can themselves be invariant while their component parts may vary synchronously. Wesson was aware of just such a possibility. He wrote:

“It is conceivable that the dimensionless numbers ... could be absolute constants, while the component parameters comprising them are variable. The possibility of such a conspiracy between the dimensional numbers was recognised by Dirac (see Harwit 1971).” [43, 44]

A simple example can be shown with the number “12.”  The total of 12 will remain constant whether we get there by 1 x 12, 2 x 6, or 3 x 4.  In the same way, hc can remain constant if h increases at the same time c decreases, or vice versa.

Measured Variation in the Speed of Light, c

From the mid 1800’s until the 1940’s, there was ongoing, and sometimes passionate, discussion in scientific journals regarding the fact that the speed of light had been measured as progressively changing. The data which indicated this were the result of hundreds of experiments by a number of methods over many years. Even physicists who had a strong preference for the constancy of atomic quantities were forced to agree with Dorsey's admission:

“As is well known to those acquainted with the several determinations of the velocity of light, the definitive values successively reported … have, in general, decreased monotonously from Cornu’s 300.4 megametres per second in 1874 to Anderson’s 299.776 in 1940…” [45]

Dorsey's re-working of the data was not able to avoid that conclusion.

In 1927, M.E.J. Gheury de Bray made an initial analysis of the speed of lightdata [46].  By April of 1931, after four new determinations, he stated

“If the velocity of light is constant, how is it that, INVARIABLY, new determinations give values which are lower than the last one obtained. … There are twenty-two coincidences in favour of a decrease of the velocity of light, while there is not a single one against it” [46].

Later that year he said,

“I believe that in any other field of inquiry such a discrepancy between observation and theory would be felt intolerable” [46].

The c values that Birge, the “keeper of the constants” at UC Berkeley, recommended be accepted in 1941 [47] are plotted in Fig. 3.

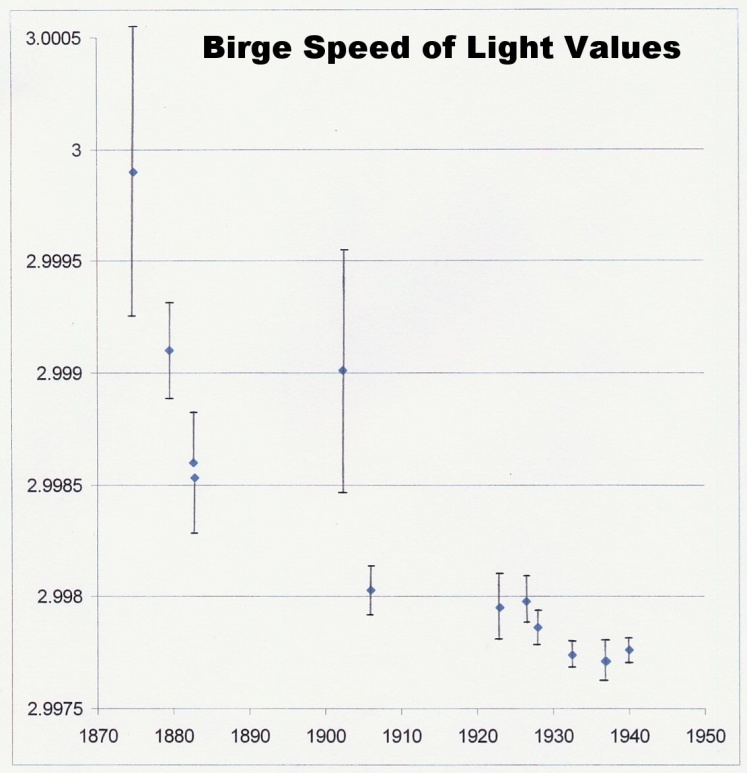
Fig. 3.  Experimental c values accepted by Birge

In all, thousands of individual experiments, using 16 methods over 330 years resulted in the 163 determinations of c as published in science journals.  These data were documented along with the synchronously changing atomic constants in our initial Report in 1987 [31].  Analysis there showed that the results from each individual method statistically supported a decline in the measured value of the speed of light.  Additionally, all data taken together also revealed that decline. In 1993, Alan Montgomery and Lambert Dolphin did an independent data analysis and came to the same conclusion in an article “Is the Speed of Light Constant in Time?” [48] The graph of 144 speed of lightvalues which had errors that were less than 0.1% (the “best” values), appears in Fig. 4.

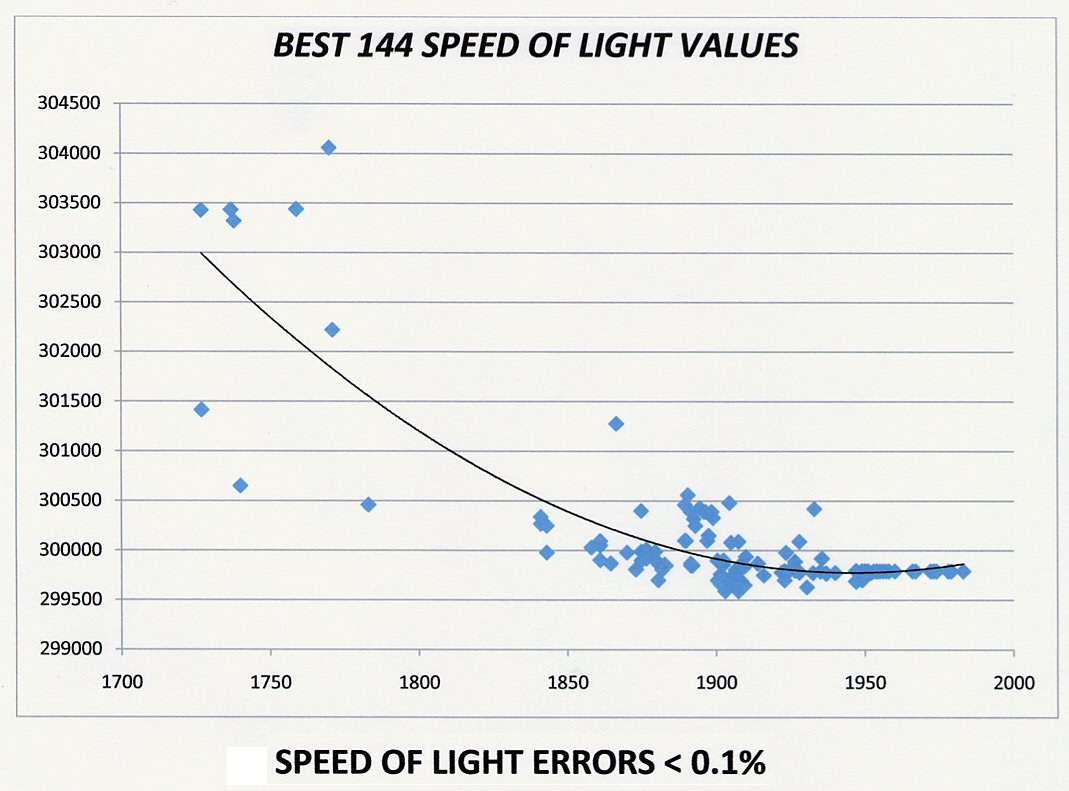
Fig. 4.  Speed of light data with errors less than 0.1%

What we see in Figs. 1 and 2 for Planck’s constant, h, and in Figs. 3 and 4 for lightspeed, c, is not what would be seen if the only cause for change was due to apparatus whose precision and accuracy were increasing. If increasing accuracy had been the cause, we should see a scatter of data points around the true value, not the one-sided approach seen in these four figures.

Again, a flat point is noted in the data around 1970. It is possible that this consistent feature of the data is associated with the oscillation modes of the cosmos as suggested by Narlikar and Arp. Once the ZPE had built to its maximum, a contracting phase in the universal oscillation would mean the same amount of ZPE would be held in a smaller volume and so its strength would appear greater. The converse is also true. All ZPE-dependent quantities would be affected. In Fig. 5 two modes of oscillation of a system are shown, represented by the red and dark blue lines. However, since oscillation modes are additive, the combined overall oscillation, shown by the light blue line, reveals resultant flat regions. The modes of oscillation of the cosmos are most likely more complex than this illustration. More data and time are needed to determine the precise form of this oscillation.

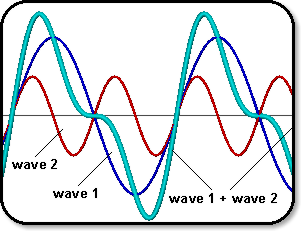
Fig. 5.  Two oscillation modes (red & dark blue) combine to give a flat point.

A change in light speed, however, does not mean a change in wave lengths. Visualize an extremely long series of waves of fixed wavelength extending to us from some very distant astronomical object in a vacuum in which the ZPE is smoothly increasing. Because the ZPE is increasing homogeneously throughout the whole cosmos, the whole train of waves is slowing simultaneously. This means the horizontal distance between the wave crests remains the same. Only the frequency, the number of waves passing a given point in a unit of time, will drop. It is rather like a long train slowing down.  The size of the individual cars does not change, but the number of cars passing the observer becomes fewer in any given amount of time. Therefore, in the wave equation c = f W, where c is lightspeed, f is frequency and W is wavelength, a constant. This means that

f  ~  c.                                                (9)

Martin and Connor point out that there is no refraction or “bending” of the light beam if the wavelengths remain constant or are not “bunched up” in the new medium [49]. This means that there will be no refraction of light with any universal ZPE changes, since wavelengths remain constant with all of them.

The ZPE, Atomic Masses and Atomic Time

The ZPE Origin for Atomic Mass

In order to understand how the ZPE affects atomic time, atomic mass has to be defined.  There are a number of problems associated with standard models for atomic masses. Many modern theories envisage the sub-atomic particles (which Feynman referred to as ‘partons’) making up matter as being charged point particles with a form but no intrinsic mass. While this may seem strange initially, it forms the basis of physics research. This concept originated with the long line of investigators, including Planck and Einstein, who developed radiation theory based on the behavior of mass-less charged point particle oscillators. Since the resulting radiation theory was in agreement with the data, the problem was then to understand how mass was imparted to these mass-less oscillators, and hence to all matter.

The problem was basically overcome after 1962, with the development of Stochastic Electrodynamics (SED physics). Contrary to Quantum Electrodynamics (QED physics), SED physics accepts a real physical Zero Point Energy.  It is seen as pervading the whole cosmos, instead of it being a mere mathematical abstraction.

SED considers the ZPE itself as the agency that imparts mass to all subatomic particles. SED physicists note that the electromagnetic waves of the ZPE impinge upon all charged, massless particles. This causes them to jitter in a random manner similar to what we see in the Brownian motion of a dust particle bombarded by molecules of air. Schrödinger referred to this “jitter motion” by its German equivalent word, Zitterbewegung.  Dirac pointed out that the Zitterbewegung jitter occurs either at, or very close to, the speed of light. This conclusion has been sustained by recent studies and the term "ultra-relativistic" has been used to describe it [50, 51].  The physical reality of the Zitterbewegung was demonstrated experimentally in 2010 with calcium ions by Roos and colleagues; Gerritsma was the lead author of the report [52].

Hal Puthoff explains what happens according to SED physics:

“In this view the particle mass m is of dynamical origin, originating in parton-motion response to the electromagnetic zeropoint fluctuations of the vacuum. It is therefore simply a special case of the general proposition that the internal kinetic energy of a system contributes to the effective mass of that system.” [53] As a result, it has been stated that, even if it is found to exist, “the Higgs might not be needed to explain rest mass at all. The inherent energy in a particle may be a result of its jittering motion [caused by the ZPE]. A massless particle may pick up energy from it [the ZPE], hence acquiring what we think of as rest mass.” [54]

The mathematical calculations of SED physicists quantitatively support this view.

The formulations of Haisch, Rueda and Puthoff show the parton’s rest mass, m, of ZPE origin is given by the equation [55, 56].

m = Γhω²/(4π²c²) ~ U² ~ h² ~ 1/c²                        (10)

In Eq. (10), ω  is the Zitterbewegung oscillation frequency of the particle, while Γ is the Abraham-Lorentz damping constant of the parton. The proportionalities in (10) hold because the terms [Γhω²] which make up the numerator of (10) can be shown to remain constant in a changing ZPE scenario [57].  From (10) it can be seen that energy, E, will be conserved with any change in ZPE strength since atomic masses are changing as the inverse square of the speed of light. Thus, energy E = mc² will remain constant.

Experimentally, the recommended values of the electron rest-mass, m, support the contention that the ZPE strength was increasing up to about 1970. The graph of these recommended values is given in Fig. 6. A similar graph could be drawn of recommended rest-mass values, m, for the proton. Again a “flat point” can be seen around 1970 supporting the Narlikar-Arp oscillation suggestion.

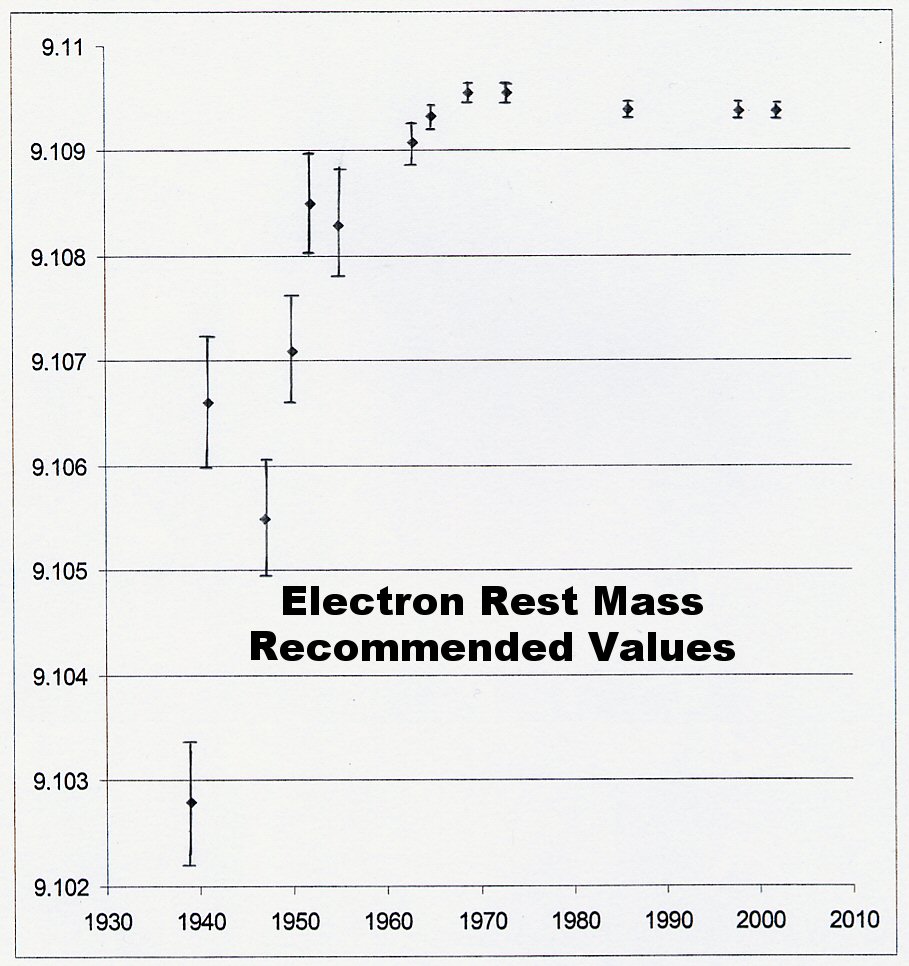
Fig. 6.  Recommended values of electron rest mass, m [17-29]

Atomic Frequencies and Atomic Clocks

From 1750 to 1960 light-speed was measured as varying. Since the use of interferometers in the 1800’s there have been no observed changes in the standard wavelengths of light. Neither have there been fringe-shifts recorded by them. Birge admitted that this allowed only one conclusion. He said: “if the value of c … is actually changing with time, but the value of λ in terms of the standard metre shows no corresponding change, then it necessarily follows that the value of every atomic frequency ... must be changing.” [58] This is in accord with Eq. (9). In order to see why Birge’s comment is correct, let us apply (10) to electrons in orbits and nucleons in orbitals. The kinetic energy of these particles is given by ½ mv2 where v is the tangential velocity. If m varies as 1/c2 it follows that v must vary as c, since kinetic energy is conserved in an atomic environment.  Birge’s statement about atomic frequencies, f, or, inversely, atomic time intervals, t, follows logically from this, since orbit velocities show the following proportionalities:

v  ~ c  ~  f.                                           (11)

The formulation for electron velocity in the first Bohr orbit verifies this. Allen’s Astrophysical Quantities [59], gives the orbit velocity, v, as

v = 2π e² /(ε h)  ~ 1/U  ~  c.                             (12)

In (12), the proportionalities affirm French’s comment that the frequency of light emitted by an electron’s transition to the ground state orbit “is identical with the frequency of revolution in the [ground state] orbit” [60]. Therefore we see that atomic frequencies generally obey Eq. (11) in the same way that photon frequencies do in (9). This means that when c is higher, atomic frequencies are also higher. Therefore, Birge's comment that "every atomic frequency must be changing" synchronously with the speed of light is shown to be correct, even though he casually dismissed the idea without further examination [58].  When everything is considered, it can be shown that atomic clocks will tick at a rate proportional to c or, alternatively, to 1/U.

Extensive investigation reveals that gravitational clocks will keep constant time with a changing ZPE strength [89].  However, since atomic frequencies vary in a manner proportional to c, then atomic clock rates can be shown to vary against the gravitational standard. Indeed, after investigation in 1965, Kovalevsky noted that if gravitational and atomic clock rates were different, “then Planck’s constant as well as atomic frequencies would drift” [61]. These two effects have already been noted here, and the data confirm the proposition.  Observatories have noted the different clock rates. One analysis stated [62]:

“Recently, several independent investigators have reported discrepancies between the optical observations and the planetary ephemerides. The discussions by Yao and Smith (1988, 1991, 1993)[63 - 65], Krasinsky et al. (1993) [66], Standish & Williams (1990) [67], Seidelman et al. (1985, 1986) [68 - 69], Seidelman (1992) [70], Kolesnik (1995, 1996) [71 - 72], and Poppe et al. (1999) [73] indicate that [atomic clocks had] a negative linear drift [slowing] before 1960, and an equivalent positive drift [speeding up] after that date. A paper by Yuri Kolesnik (1996) reports on positive drift of the planets relative to their ephemerides based on optical observations covering thirty years with atomic time. This study uses data from many observatories around the world, and all observations independently detect the planetary drifts. … [T]he planetary drifts Kolesnik and several other investigators have detected are based on accurate modern optical observations and they use atomic time. Therefore, these drifts are unquestionably real.” [62]

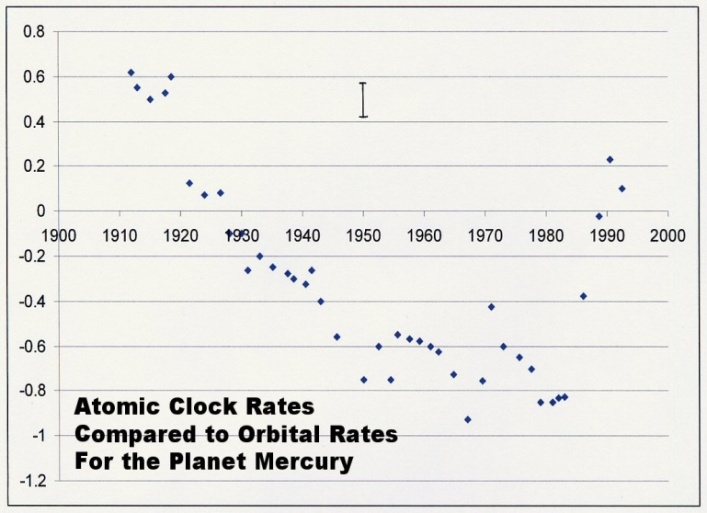
Fig. 7.  Atomic clock rates on the y-axis compared to orbital rates.

Fig. 8.  Atomic clock rates (y-axis) compared to orbital rates using solar data from 1910 to 1999. The scale is approximately the same as for Fig. 7.

Some typical data are plotted in Figs. 7 and 8.  There the vertical axis is effectively the atomic clock rate while the horizontal axis is our orbital dates.  The data turn-around which occurred around 1970 is again apparent in these figures.

Figs. 7 and 8 are to approximately the same scale [62].  This turnaround, which is now apparent in all the ZPE-dependent data, can be attributed to the change in the Narlikar-Arp oscillation mode of the cosmos.

The ZPE and the Redshift

The ZPE and Atomic Orbits

The Zero Point Energy is not only responsible for the slowing of both light and atomic clocks, it also provides the answer to a problem found in classical physics. Classical physics requires an electron orbiting a nucleus to be radiating energy.  Losing energy, it would then seem to have to spiral into the nucleus. This does not happen. Interestingly, the all-pervasive ZPE ‘sea’ has been shown to maintain the stability of atomic orbits across the cosmos.  According to SED physics, the electron’s loss of energy must be coupled with the energy that it absorbs from the ZPE. A stable orbit then results when the energy radiated by the electron exactly matches the energy absorbed from the ZPE.

Quantitative analyses of this effect were done, and the results summarized by stating that

“Boyer [74] and Claverie & Diner [75] have shown that if one considers circular orbits only, then one obtains an equilibrium [orbit] radius of the expected size [the Bohr radius]: for smaller distances, the electron absorbs too much energy from the [ZPE] field…and tends to escape, whereas for larger distances it radiates too much and tends to fall towards the nucleus.” [76]

In 2006 , Spicka et al. noted that

"It is an enormously fruitful idea developed in the frame of SED physics that the moving charged particle, electron for example, can be kept on a stationary orbit in consequence of dynamical equilibrium between absorbed ZPR [Zero-Point Radiation] and emitted recoil radiation.” [77]

Spicka et al. then go on to illustrate that an electron moving in an orbit around a proton is under the influence of its electrostatic attraction. As it orbits, the electron undergoes a series of elastic collisions with the impacting waves of the ZPE which perturb the orbit. These impacting waves force the electron to change direction. The whole 'orbit' then becomes composed of a series of essentially straight line segments whose direction is continually being changed by the impact of these ZPE waves.

Every time the electron is impacted by the ZPE, it emits recoil radiation, just as classical physics requires. Calculations based on the Compton frequency reveal that the electron may receive over 18,700 hits from the ZPE waves for every orbit around the nucleus. It is these hits which cause the uncertainty in both the position of the electron and its actual orbit around the proton. This is the cause of the uncertainty that Heisenberg hypothesized.

For a stable orbit, the power absorbed by the electron from the ZPE wave collision must be equal to the power emitted by the electron's recoil radiation. When the ZPE is stronger, there are more ZPE waves per unit volume and so there are more hits per second on the electron as it travels in its orbit. This means that the electron is now emitting more recoil radiation, and so has a tendency to move towards the nucleus as pointed out in the above quote from reference [77].  The means that the orbit radius, r, will tend to decrease. But the wavelengths of emitted light, W, depend on orbit radius r since the standard equation has [59, 60]

W  = (1/2)(e²/ε)(hc/1)(r/1).                             (13)

We have seen that both (ε/e²) and (hc) are invariant with increasing ZPE strength, U.  From (13) it is then seen that the emitted wavelengths, W, are directly proportional to the orbit radius, r, so we can write

W  ~  r.                                             (14)

Consequently, an increasing ZPE strength will result in both atomic orbits and the wavelengths of emitted light decreasing. Shorter wavelengths mean bluer light. This means that as the ZPE increased, atoms emitted light which was intrinsically bluer.

This is why, as we look farther out into space (and thus further back in time), we would expect to see light progressively shifted toward the red end of the spectrum.  This is, in fact, what we do see. This redshift is a feature of astronomical observations.

The usual explanation for the redshift is that it is a Doppler effect produced by an expanding universe.  If this were the case, all spectral lines of emitted light should be significantly broadened; they are not. Also, we should see the redshift measurements increasing smoothly with distance. That is not seen either. What is seen are narrow spectral lines, and redshift measurements that come in groups, or quantities, with no intervening measurements.  This is referred to as the quantized redshift.

Because every atomic orbit must exactly accommodate the de Broglie wavelength of the orbiting electron, it can be shown that a quantized redshift results from the orbit changes caused by an increasing ZPE. When followed through, the values of the quantization observed by Tifft [78], Arp [79], Guthrie & Napier [80-82], and others can be accurately reproduced. A graph of some of Guthrie and Napier’s results is in Fig. 9.

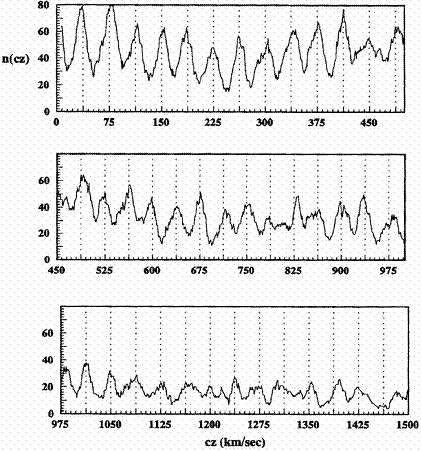
Fig. 9.  Guthrie and Napier's redshift quantization results for 1996 expressed as speeds of recession (cz) in km/sec. The peaks in the graph show where quantum steps occur in multiples of 37.5 km/sec.

The Behavior of the ZPE Through Time

The idea of universal expansion is thus negated by the hydrogen cloud data, the un-broadened spectral lines, and quantized redshift data.  Since the redshift is the result of an increase in ZPE strength, it can then give us information as to how the ZPE strength built up over the lifetime of the cosmos. When this analysis is complete, the ZPE strength, U, and redshift, z, are related in the following way:

1/U = K(1 + z) = 4.745 x 10⁹ [(1 + x)/√(1 – x²)]             (15)

In (15) the constant of proportionality, K, is related to the square-root of the Compton frequency and another factor.  In (15), the distance x is a fraction so that x = 0 where the redshift function ends close to, or in, our galaxy, and x = 1 at the distance that corresponds with the inception of the cosmos. Looking out into space at progressively more distant galaxies is equivalent to looking further back in actual orbital time, T. Since we take orbital time as passing in a linear fashion, and since distance is also linear, we can substitute orbital time, T, for distance, x, giving

(1 + z)  =  [(1 + T) /√ (1 – T²)].                          (16)

In Eq. (16), T is in orbital time such that T = 1 at the origin of the cosmos while we have T = 0 when the redshift function ceases at a position in space in, or near, our galaxy. This is exactly in line with the treatment for x. Therefore the behavior of ZPE-dependent quantities over time follows the relationship in Eq. (17) below which is graphed in Fig. 10.

1/U ~1/h ~ c/1 ~f  ~ 1/t ~ 1/√m ~ K(1 + z) = K[(1 + T)/√(1 – T²)]   (17)

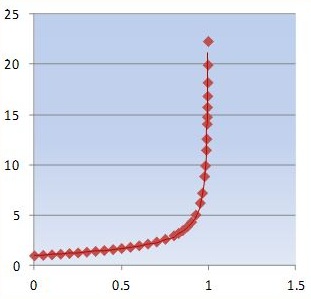
Fig. 10.  Graph of behavior of lightspeed c, atomic clock rates and frequencies, f, and redshift z with orbital time T horizontally. The scale of the vertical axis follows redshift which must be multiplied by constant K for the other quantities.

Implications in Other Disciplines

Implications for Plasma Physics

Around 1990, plasma physics opened up new vistas in astronomy based on interacting electric and magnetic fields in plasma filaments in contrast to gravitational interactions [83, 84].  Experimentation with plasma filaments in laboratories have shown that the electric and magnetic interactions in these filaments form, in miniature, all the various shapes of galaxies that astronomy is familiar with. One set of experiments using the interaction of two plasma filaments produced the miniature galaxies shown in Fig. 11 at the bottom. These laboratory results can be compared with the galaxies we see out in the cosmos. Bennett pinches on plasma filaments forms stars like beads on a string. This is shown in miniature in the last three frames of Fig. 11 at the bottom, and in reality in the galaxy M81 at the top. Similar processes form planets.

Fig. 11.  Top: Spitzer telescope image of galaxy M81. Bottom: Looking down the long axis of two interacting plasma filaments in the lab which produced miniature galaxies. Simulations included up to 12 interacting filaments, but all galaxy types can be produced with two or three filaments. Compare with M81 at top: Stars form along plasma filaments making up the spiral arms like beads on a string due to plasma pinch effects, like the 3 final frames at bottom.

The magnitude of the electric and magnetic interactions which form galaxies, stars and planets is dependent upon the strength of the Zero Point Energy (ZPE). With an increase in the ZPE strength over time, it can be shown that voltages were reduced, as were current strengths and the speed of plasma interactions. Resistances remained unaltered, while capacitances increased in proportion to U [85].  Analysis also indicates that a lower ZPE in earlier times resulted in filaments approaching each other and interacting more quickly than now.  This would have speeded up galaxy formation. The faster accumulation of material coupled with instabilities from pinches in the filaments also resulted in more rapid star and planet formation.  More efficient Marklund convection, which sorts elements in filaments in order of ionization potential, resulted in the layered structures of planets as well as the differences in their relative compositions out from the sun [85].

Higher currents and voltages in the earlier days of our solar system may have caused the planetary plasma-spheres (magnetospheres) to go into glow mode and be very visible.  Planetary alignments may then have resulted in massive electrical discharges between the planets. There is a persistent theme in myths and legends regarding both planetary gods in the sky (visible plasma-spheres), as well as massively destructive ‘thunderbolts’ associated with them which inspired terror in the people. Higher currents and voltages in the past might also have been responsible for electromagnetic effects which studies show could have resulted in some structures on planetary surfaces [96].  In other words, a lower ZPE in the past, combined with plasma physics, may be offering an entirely different explanation for some things.

Support from the Fossil Record

The Zero Point Energy has been shown to be responsible for a number of astronomical effects.  However there may also be something else it is at least partially responsible for.  We have been puzzled for many years by gigantism in the fossil record.  The giant dinosaurs were prominent in the Mesozoic Era. But earlier, in the Paleozoic, we see evidence of giant sea-scorpions and giant millipedes, both over 2 meters long. In the more recent Cenozoic Era, a giant wombat, the size of a rhinoceros, may have been the largest marsupial to ever inhabit Earth. Similarly, many early plant types grew to extraordinary sizes. In contrast, the plants and animals in our world now are often very much smaller.  How could the ZPE be implicated in this?

Nerves in all vertebrate animals, including humans, operate by conducting electrical impulses.  In the same way a wire must be insulated to keep the electrical current from dissipating, nerves in most vertebrate species are insulated by a fatty layer called myelin. This myelin coating allows the nerve impulses to travel at a high speed in one direction and not be dissipated in all directions. This speed rises from about 1 meter per second for a bare nerve fiber, about 10 microns in diameter, to over 50 meters per second for the same axon (nerve fiber) sheathed in myelin. (A micron is one millionth of a meter.)

Fig. 12.  Typical nerve cell (neuron). Schwan's cells make myelin.

In contrast, the invertebrates, like the giant sea scorpions, the monster millipedes and the immense dragonflies, all had non-myelinated nerves. The rate of nerve transmission today appears to limit the size of these organisms to about 30 centimeters. Yet to survive, animals must have an efficient nervous system which conducts nerve impulses sufficiently rapidly for them to have a viable reaction time. How was this achieved with the larger animals of the past?

This is where the importance of bio-electro-magnetism arises. J. Malmivuo and R. Plonsey have made some key comments which have a bearing on our problem. In [86], page 33, they state:

"All cells exhibit a voltage difference across the cell membrane. Nerve cells and muscle cells are excitable. Their cell membrane can produce electrochemical impulses and conduct them along the membrane. In muscle cells, this electric phenomena is also associated with the contraction of the cell [the working of the muscle]. In other cells, such as gland cells and ciliated cells, it is believed that the membrane voltage is important to the execution of cell function."

These authors [page 42, Eq. (2.1)] show that the axon’s nerve signal velocity is inversely proportional to its capacitance. Mathematically, all other terms which would be variable under changing ZPE conditions cancel out. This leaves axon capacitance as the sole player where nerve conduction velocities are concerned. When the ZPE strength was lower, and all voltages intrinsically higher, currents were stronger, and capacitances lower. Thus, when the ZPE strength was 1/10th of its current value, so also was the capacitance of the axons. This meant nerve signals were not only stronger, but traveled 10 times as fast down the axon.  So both nerve signal velocities and reaction times would have been much faster as in the past [87].  If the rate of nerve transmission is, indeed, one of the factors affecting the final size of an organism, a lower ZPE might have been one reason for the gigantism of the past. To put it another way, the high ZPE strength of today necessitates small sizes for animals now.

A parallel situation exists with fossil plants. Their great size and prolific numbers in the past suggest that some factor involving photosynthesis has changed. Photosynthesis depends on light and light is affected by the Zero Point Energy. Examination of this option reveals some pertinent facts [87].

As previously demonstrated [87], when the ZPE was lower, the production rate of light waves (or photons) by the sun and stars was higher in inverse proportion [85]. This holds whether nuclear or electric processes are involved [85]. Thus, when the ZPE strength was 1/10th of what it is today, the speed of light was 10 times higher, meaning the earth received 10 times as many waves or photons per second as it does now. However this did not damage anything because the high number was offset by the fact that the electric and magnetic properties of the vacuum would have had only 1/10th of their current value. Since it is these properties that govern the intensity or brightness of the waves or photons, each only had 1/10th of the intensity that it has today. Therefore, even though there were 10 times as many photons or waves, the total intensity or brightness of light would have been the same as today. Note that the energy of each photon or wave (that is, its color) would have been the same [85, 87].

When the ZPE was low, plants received more photons of light of a given color (energy) per unit area per second than they do now. Under these conditions, analysis indicates that photosynthetic processes would have been more efficient when the ZPE was lower, so that plants would have grown more rapidly and to enhanced sizes.

As we then examine the effects of a lower Zero Point Energy in the past, it becomes evident that they may not have been confined to “outer space.”  More efficient photosynthesis in plants and more efficient nerve transmissions in animals both would have been the result of a lower ZPE.  This may well have contributed to the gigantism we see in the fossil record.  Put another way, the gigantism we see among fossils may itself be testimony to a lower ZPE in the past.

The ZPE and Relativity

The Concept of the “Ether”

At the beginning of the twentieth century, it was assumed that there had to be a medium filling the vacuum of space so that light waves could be transmitted. This ‘light carrying medium’ was called the ether (or aether). It was assumed that the ether was universally at rest. As a result of the orbital motion of the earth through this stationary ether, it was then thought possible to detect the "ether drift" past the earth. The simplest way of doing this was to send beams of light in different directions and measure the difference in light speed as it traveled either with or against the ether drift by using fringe shifts in an interferometer. This experiment could be performed since the orbital speed of the earth is about 30 km/s, and this velocity difference was measurable by the proposed interferometer fringe shifts. Michelson and Morley (M-M) performed this experiment in 1881 and the only drift recorded, about 8 km/s, was considered by most to be near the error limits of the equipment. As a consequence, the official position has been that no drift was recorded.

In order to account for this lack of motion through the stationary ether, a number of proposals were made by a variety of physicists, including Fitzgerald, Lorentz and Einstein. Even as late as 1929, Einstein was stating in his lectures that, though the ether was still considered to exist, the theory of relativity explained why no "ether drift" was detected. He proposed that there were changes in space and time, and that there was no absolute frame of reference against which anything could be measured. That was the prime reason for his special theory of relativity (SR), which later opened up the way for the general theory of relativity (GR). Historically, Einstein's theory was accepted as the explanation.

The ZPE is the all-pervasive ‘light carrying medium’ or ‘ether’ that exists in reality. Its properties are vastly different from those imagined by physicists when the Michelson-Morley experiment was done. One key property of the ZPE was discussed by Timothy Boyer in his article, “The Classical Vacuum” as follows [88]:

“It turns out that the zero-point spectrum can only have one possible shape…the intensity of the radiation at any frequency must be proportional to the cube of that frequency. A spectrum defined by such a cubic curve is the same for all unaccelerated observers, no matter what their velocity; moreover, it is the only spectrum that has this property.”

Increasing Masses and Slowing Clocks

It is known that Einstein's relativity has made predictions that proved correct. However these same predictions can be made using intuitive concepts from the ZPE approach and very much simpler mathematics in the process [89].

Special Relativity deals with how velocities affect moving objects. As velocities increase, atomic masses also increase and atomic clocks slow. We have observed that the acceleration of an electron through a linear accelerator results in an increase in mass of the electron. This has been hailed as proof that relativity is correct. However, the SED approach predicts exactly the same effect as a result of the existence of the ZPE. The SED approach has shown that the masses of sub-atomic particles are all results of the "jiggling" of these particles by the impacting waves of the ZPE. This "jiggling" imparts kinetic energy to these mass-less particles and this energy appears atomically as mass. An increased "jiggling" occurs when a particle is in motion, because more ZPE waves are impacting the particle than when it is at rest. An increase in particle mass is then the result. The higher the velocity, the more ZPE waves are being encountered per second and so more "jiggling" occurs and so there is a greater mass. This has been mathematically quantified by SED physicists.

In addition, as atomic masses, m, increase by this process, it can be shown that the rate of ticking of atomic clocks slows down. This occurs because kinetic energy (0.5mv2) is conserved in atomic processes. This energy conservation requires that atomic particles must move more slowly as they gain mass -- that is their velocities, v, decrease. Slowing atomic processes, in turn, then mean that atomic time slows with increases in mass. The converse is also true; atomic processes will speed up with a decrease in atomic mass (which comes from a decrease in the ZPE). Changes in atomic masses result in changes in atomic clock rates.

Bending Light in a Gravitational Field

SED physics also presents the same predictions as General Relativity (GR).  Using intuitive concepts and simple mathematics, even the awkward movements of Mercury, known as the advance of its perihelion, can be explained [89].  As early as 1920, working on an intuitive level and using simple mathematics, Sir Arthur Eddington wrote [90]:

“Light moves more slowly in a material medium than in a vacuum, the velocity being inversely proportional to the refractive index of the medium.... We can thus imitate the [GR] gravitational effect on light precisely, if we imagine the space round the sun filled with a refracting medium which gives the appropriate velocity of light. To give the velocity c(1- μ/r), the refractive index must be 1/(1- μ/r). …Any problem on the paths of rays near the sun can now be solved by the methods of geometrical optics applied to the equivalent refracting medium.”

It can be demonstrated that the build-up of the ZPE strength around collections of particles provides just such an “equivalent refracting medium”. When subatomic particles are “jiggled” by the ZPE, they send out secondary radiation which boosts the ZPE strength locally. The larger the collection of particles, the greater the local boost to the ZPE becomes. Since a stronger ZPE means a slowing of light photons and waves in their travel, then the boosted ZPE acts as an ‘equivalent refractive medium’. Refraction occurs in this case because the ZPE strength changes locally, not in a uniform or simultaneously manner across the entire universe. It is this local change in the ZPE which bends the rays of light. Since this effect only occurs in the vicinity of a massive collection of jiggling particles, its cause is attributed to the “gravitational field.”

Is There an Absolute Reference Frame?

Einstein’s basic postulate, from which the theory of relativity takes its name, is that there is no absolute frame of reference anywhere in the universe. However, in 1964 the Cosmic Microwave Background Radiation (CMBR) was discovered by Penzias and Wilson. The physical reality of the CMBR has provided an absolute rest frame against which the actual velocity of the solar system, our galaxy, and our Local Group of galaxies can be measured. Cosmologist and astronomer, Martin Harwit. writes [91]:

“Current observations indicate that the universe is bathed by an isotropic bath of microwave radiation. It is interesting that the presence of such a radiation field should allow us to determine an absolute rest frame on the basis of local measurement.”

Harwit then goes on to salvage what he can for relativity by saying

”...the establishment of an absolute rest frame would emphasize the fact that special relativity is really only able to deal with small-scale phenomena and that phenomena on larger scales allow us to determine a preferred frame of reference in which cosmic processes look isotropic.”[91]

In other words, special relativity applies at an atomic level but not a macroscopic one. This is discussed in more detail in the full Report.

Gravity, General Relativity and the ZPE

Finally, there is the question of what gravity really is. While it may be correct to state that GR is a good mathematical model, that is not the same as explaining how gravitational forces originate. The GR model is often presented using the "rubber sheet" analogy. In this analogy, the picture is often given of a heavy ball-bearing, representing a massive body like the earth or sun, which deforms the surface of a rubber sheet (space-time) and causes it to curve. The problems with both the mathematics and the analogy were mentioned by Tom Van Flandern and others at a conference in 2002. It was described as follows [92]:

"In the geometric interpretation of gravity, a source mass curves the ‘space-time’ around it, causing bodies to follow that curvature in preference to following straight lines through space. This is often described by using the ‘rubber sheet’ analogy ... However, it is not widely appreciated that this is a purely mathematical model, lacking a physical mechanism to initiate motion. For example, if a ‘space-time manifold’ (like the rubber sheet) exists near a source mass, why would a small particle placed at rest in that manifold (on the rubber sheet) begin to move towards the source mass? Indeed, why would curvature of the manifold (rubber sheet) even have a sense of ‘down’ unless some force such as gravity already existed? Logically, the small particle at rest on a curved manifold would have no reason to end its rest unless a force acted on it. However successful this geometric interpretation may be as a mathematical model, it lacks physics and a causal mechanism."

This problem was also noted by Haisch and his colleagues at the California Institute for Physics and Astrophysics (CIPA). They say [93]:

“The mathematical formulation of GR represents spacetime as curved due to the presence of matter and is called geometrodynamics because it explains the dynamics (motions) of objects in terms of four-dimensional geometry. Here is the crucial point that is not widely understood: Geometrodynamics merely tells you what path (called a geodesic) that a freely moving object will follow. But if you constrain an object to follow some different path (or not to move at all) geometrodynamics does not tell you how or why a force arises. … Logically you wind up having to assume that a force arises because when you deviate from a geodesic you are accelerating, but that is exactly what you are trying to explain in the first place: Why does a force arise when you accelerate? … this merely takes us in a logical  full circle.”

In view of these shortcomings, alternative proposals need to be examined. One of these comes directly from SED physics as a result of the ZPE. It involves the positively and negatively charged virtual particles of the vacuum.  SED physicists have noted that all charged partons in the universe undergo the Zitterbewegung jostling through interaction with the ZPF. These fluctuations are relativistic so that the charges move at velocities close to that of light. Haisch, Rueda and Puthoff then say [94]:

“Now a basic result from classical electrodynamics is that a fluctuating charge emits an electromagnetic radiation field. The result is that all charges in the universe will emit secondary electromagnetic fields in response to their interactions with the primary field, the ZPF. The secondary electromagnetic fields turn out to have a remarkable property. Between any two [charged] particles they give rise to an attractive force. The force is much weaker than the ordinary attractive or repulsive forces between two stationary electric charges, and is always attractive, whether the charges are positive or negative. The result is that the secondary fields give rise to an attractive force we propose may be identified with gravity. … Since the gravitational force is caused by the trembling motion, there is no need to speak any longer of a gravitational mass as the source of gravitation. The source of gravitation is the driven motion of a charge, not the attractive power of the thing physicists are used to thinking of as mass.”

This may be explained as follows. First, there is the bare charge which is intrinsic to the electron or parton. The mere existence of this charge polarizes the vacuum. For a negative electron, the layer of virtual particles next to the electron will tend to be positive charges, then a layer of negative charges next to that, and so on. This vacuum polarization acts to attract other partons and/or electrons which may be nearby. The sign of the charge does not matter; it only affects the phase of the interactions.

However, that is only the first step. This same charge is also undergoing the Zitterbewegung which gives it its atomic mass from the kinetic energy of the ‘jitter.’ In this case, there is the also polarization which arises from the jitter itself.  This arises because the random acceleration, imparted by the impacting ZPE waves to the jittering partons or electrons, causes them to emit secondary radiation. This secondary radiation locally boosts the strength of the ZPE, which in turn causes more virtual particle pairs to come into existence per unit volume proportional to ZPE strength, U. This results in a stronger polarization than if the parton or electron was at rest with no secondary radiation. Therefore, around this charge which is jittering, there is a double polarization effect. This net attractive force between the partons and electrons has been shown by SED physicists to be quantitatively identical to gravity.

It follows, then, that where there are many particles, there are many intrinsic charges undergoing the jitter of the Zitterbewegung.So the larger the collection of particles, the stronger is the resulting attraction we call gravity. Haisch concluded his explanation when he said, “This might explain why gravity is so weak. One mass does not pull directly on another mass but only through the intermediary of the [charged virtual particles that make up the] vacuum.” [95]  On this basis, then, gravitation and mass may be considered to be simply manifestations of electromagnetic effects linked with the ZPE.

While QED physics has treated the Zero Point Energy as a mathematical abstraction, SED physics has accepted it as a measureable reality. Its existence is considered by some to explain gravity itself. Evidence points to an increase in the ZPE through time, and it is this change which has affected light speed, atomic masses, and atomic clocks.   This change also affected the interactions of the plasma filaments in space, allowing galaxies, stars and planets to be formed much more quickly than gravity allows.  Additional evidence points to the influence the changing ZPE had on life on Earth in the past, producing the gigantism we see in the fossil record.  In short, it can be seen that SED physics with a real Zero Point Energy, which has increased with time, holds potential answers to a number of problems that science currently faces in a multitude of disciplines.

[ 1 ]   M. Planck, Verhandlungen der Deutschen Physikalischen Gesellschaft 13: 138 (1911).
[ 2 ]   A.  Einstein, O. Stern, Ann. Physik 40: 551 (1913).
[ 3 ]   W. Nernst, Verhandlungen der Deutschen Physikalischen Gesellschaft 4: 83-116 (1916).
[ 4 ]   U. Mohideen, A. Roy, Phys. Rev. Lett. 81: 4549 (1998).
[ 5 ]   L. Ashmore, in F. Potter, Ed., 2nd Crisis in Cosmology Conference, CCC-2, ASP Conference Series 413: 3 (Proceedings of the Conference held 7-11 September 2008, at Port Angeles, Washington, USA, Astronomical Society of the Pacific, San Francisco, 2009).
[ 6 ]   L. Ashmore, “An Explanation of Redshift in a Static Universe”, Proceedings of the NPA 7: 17-22 (Long Beach, CA, 2010).
[ 7 ]   C. H. Gibson, “Turbulence and Mixing in the Early Universe”, Keynote Paper, International Conference Mechanical Engineering, Dhaka, Bangladesh, Dec. 26 to 28, 2001, http://arxiv.org/abs/ astro-ph/0110012, retr. 4/15/10.
[ 8 ]   F. Hoyle, G. Burbidge, J. Narlikar, A Different Approach to Cosmology, p. 108 ff. (Cambridge University Press, Cambridge, 2005).
[ 9 ]   C. Bizon et al, in J. Karkheck, Ed., Dynamics: Models and Kinetic Methods for Non-equilibrium Many Body Systems (Kluwer, Dordrecht, 1999).
[ 10 ] H. E. Puthoff, Phys. Rev. A 40 (9): 4857 (1989); also Science Editor, New Scientist, p. 14 (2 Dec 1989).
[ 11 ] J. Narlikar & H. Arp, Astrophysical Journal 405: 51 (1993).
[ 12 ] L. de Broglie, New Perspectives in Physics (Basic Books Publishing Co., New York, 1962).
[ 13 ] E. Nelson, Phys. Rev. 150: 1079 (1966); Also, Dynamical Theories of Brownian Motion (Princeton University Press, 1967).
[ 14 ] T. H. Boyer, Phys. Rev. D 11: 790 (1975).
[ 15 ] M. R. Wehr, J. A. Richards, Physics of the Atom, p. 37 (Addison Wesley, 1960).
[ 16 ] B. Haisch, A. Rueda, Phys. Lett. A 268: 224 (2000).
[ 17 ] F.G. Dunnington, “The Atomic Constants”, Reviews of Modern Physics 11 (2): 65-83 (Apr 1939).
[ 18 ] R. T. Birge, “A New Table of Values of the General Physical Constants”, Reviews of Modern Physics 13 (4): 233-239 (Oct 1941).
[ 19 ] J. W. M. DuMond, E. R. Cohen, “Our Knowledge of the Atomic Constants F, N, m and h in 1947, and of Other Constants Derivable Therefrom”, Reviews of Modern Physics 20 (1): 82-108 (Jan 1948).
[ 20 ] J. A. Bearden, H. M. Watts, “A Re-Evaluation of the Fundamental Atomic Constants”, Physical Review 81: 73-81 (Jan 1951).
[ 21 ] J. W. M. DuMond, E. R. Cohen, “Least Squares Adjustment of the Atomic Constants, 1952”, Rev. Mod. Phys. 25 (3): 691-708 (Jul 1953).
[ 22 ] E. R. Cohen et al, “Analysis of Variance of the 1952 Data on the Atomic Constants and a New Adjustment, 1955”, Reviews of Modern Physics 27 (4): 363-380 (Oct 1955).
[ 23 ] E. R. Cohen, J.W. M. DuMond, “Present Status of our Knowledge of the Numerical Values of the Fundamental Constants”, in W. H. Johnson, Jr., Ed., Proceedings of the Second International Conference on Nuclidic Masses, pp. 152-186 (Vienna, Austria, July 15-19, 1963, Springer-Verlag, Wien, 1964).
[ 24 ] E. R. Cohen, J. W. M. DuMond, “Our Knowledge of the Fundamental Constants of Physics and Chemistry in 1965”, Reviews of Modern Physics 37 (4): 537-594 (Oct 1965).
[ 25 ] B. N. Taylor, W. H. Parker, D. N. Langenberg, “Determination of e/h Using Macroscopic Quantum Phase Coherence in Superconductors: Implications for Quantum Electrodynamics and the Fundamental Physical Constants”, Reviews of Modern Physics 41 (3): 375-496 (Jul 1969).
[ 26 ] E. R. Cohen, B. N. Taylor, “The 1973 Least-Squares Adjustment of the Fundamental Constants”, Journal of Physical and Chemical Reference Data 2 (4): 663-718 (1973).
[ 27 ] E. R. Cohen, B. M. Taylor, “The 1986 Adjustment of the Fundamental Physical Constants”, Codata Bulletin 63 (Pergamum Press, Nov 1986).
[ 28 ] P. J. Mohr, B.N. Taylor, “Codata Recommended Values of the Fundamental Physical Constants, 1998”, Rev. Mod. Physics (Apr 2000).
[ 29 ] http://physics.nist.gov/constants 6, retr. 6 Jun 2011.
[ 30 ] J. H. Sanders, The Fundamental Atomic Constants, p. 13 (Oxford University Press, Oxford, 1965).
[ 31 ] T. Norman, B. Setterfield, The Atomic Constants, Light, and Time, Research Report, p. 35 (Stanford Research Institute (SRI) International & Flinders University, South Australia, Aug 1987).
[ 32 ] J. N. Bahcall, E. E. Salpeter, Astrophys. J. 142: 1677-1681 (1965).
[ 33 ] W. A. Baum, R. Florentin-Nielsen, Astrophys. J. 209: 319-329 (1976).
[ 34 ] J. E. Solheim, T.G. Barnes, H.J. Smith, Astrophys. J. 209: 330-4 (1976).
[ 35 ] P. D. Noerdlinger, Phys. Rev. Lett. 30: 761-762 (1973).
[ 36 ] R. Srianand et al. also D. Monroe, Phys. Rev. Lett. 92: 121302 (2004).
[ 37 ] L. L. Cowie, A. Songaila, Nature, 428: 132 (2004).
[ 38 ] F. J. Dyson, Phys. Rev. Lett. 19: 1291-1293 (1967).
[ 39 ] A. Peres, Phys. Rev. Lett. 19: 1293-1294 (1967).
[ 40 ] J. N. Bahcall, M. Schmidt, Phys. Rev. Lett. 19: 1294-1295 (1967).
[ 41 ] P. S. Wesson, Cosmology and Geophysics, Monographs on Astronomical Subjects, pp. 65-66, 88-89, 115-122, 207-208 (Adam Hilger Ltd, Bristol, 1978).
[ 42 ] M. Brooks, “Operation Alpha”, New Scientist, p. 33-35 (23 Oct 2010)
[ 43 ] P. S. Wesson, op. cit., pp. 65-66, 88-89, 115-122, 207-208.
[ 44 ] M. Harwit, Bull. Astron. Inst. Czech. 22: 22-29 (1971).
[ 45 ] N. E. Dorsey, Trans. Am. Phil. Soc. 34: 1 (1944).
[ 46 ] M. E. J. Gheury de Bray, Nature 120: 602 (1927); 127: 522 (1931); and 127: 892 (1931).
[ 47 ] R. T. Birge, Rep. Prog. Phys. 8: 90 (1941).
[ 48 ] A. Montgomery, L. Dolphin, “Is the Velocity of Light Constant in Time?”, Galilean Electrodynamics 4 (5): 93ff (1993).
[ 49 ] S. L. Martin, A. K. Connor, Basic Physics, Vol. 3, 6th Ed., p. 1193 (Whitcombe and Tombs Pty. Ltd., Melbourne, Australia, 1958).
[ 50 ] B. Haisch, A. Rueda, H. E. Puthoff, Speculations in Science and Technology 20: 99-114 (1997).
[ 51 ] Science Editor, New Scientist 2611 (7 July 2007).
[ 52 ] R. Gerritsma et al, Nature 463: 68-71 (7 Jan 2010), pp. 68-71.
[ 53 ] H. E. Puthoff, Phys. Rev. A 39 (5): 2333-2342 (1989).
[ 54 ] M. Chown, New Scientist, pp. 22-25 (3 Feb 2001).
[ 55 ] B. Haisch, A. Rueda, H. E. Puthoff, Physical Review A 49 (2): 678-694 (Feb 1994).
[ 56 ] H. E. Puthoff, Phys. Rev. A 39 (5): 2333-2342 (1 Mar 1989).
[ 57 ] B. Setterfield, ”Reviewing the Zero Point Energy,” Journal of Vectorial Relativity 2 (3): 1-28 (2007) and also in reference [31].
[ 58 ] R. T. Birge, Nature 134: 771-772 (1934).
[ 59 ] A.N. Cox, Allen’s Astrophysical Quantities, p. 9 (Springer-Verlag, 2000).
[ 60 ] A. P. French, Principles of Modern Physics, p.114 (Wiley 1959).
[ 61 ] J. Kovalevsky, Metrologia 1 (4): 169-180 (1965).
[ 62 ] C. J. Masreliez, Aperion 11: 4 (Oct 2004); also Masreliez & Kolesnik, Astronomical Journal (Aug 2004); Y.B. Kolesnik, “Analysis of the secular variations of the longitudes of the Sun, Mercury, and Venus from Optical observations” (2005), http://www.estfound.org/ analysis.htm.
[ 63 ] Z-G. Yao, C. Smith in S. Debarbat et al, Eds., Mapping the Sky, p. 501 (Kluwer, Dordrecht, 1988).
[ 64 ] Z-G. Yao, C. Smith, Astrophys. and Space Science 177: 181 (1991).
[ 65 ] Z-G. Yao, C. Smith in I. I. Muller, B. Kolaczek, Eds., Developments in Astrometry and Their Impact on Astrophysics and Geodynamics, p. 403 (Kluwer, Dordrecht, 1993).
[ 66 ] G. A. Krasinsky et al, Cel. Mec. Dyn Astron55: 1 (1993).
[ 67 ] E. M. Standish, J. G. Williams, in J. H. Lieske, V. K. Abalakin, Eds., Inertial Coordinate System on the Sky, p. 173 (Kluwer, Dordrecht, 1990).
[ 68 ] P. K. Seidelman et al, in V. Szebenhey, B. Balazs, Eds., Dynamical Astronomy, p. 55 (Austin, TX, 1985).
[ 69 ] P. K. Seidelman et al, in J. Kovalevsky, V. A. Brumberg, Eds., Relativity in Celestial Mechanics and Astrometry, p. 99 (Kluwer, Dordrecht, 1986).
[ 70 ] P. K. Seidelman, in S. Ferraz-Mello et al, Eds., Chaos, Resonance and Collective Dynamical Phenomena in the Solar System, p. 49 (Kluwer, Dordrecht, 1992).
[ 71 ] Y. B. Kolesnik, Astronomy and Astrophtsics 294:  876 (1995).
[ 72 ] Y. B. Kolesnik, in S. Ferraz-Mello et al, Eds., Dynamics, Ephemerides and Astrometry of the Solar System, p 477 (Reidel, Dordrecht, 1996).
[ 73 ] P. S. R. Poppe et al, Astronomical Journal 116: 2 (1999).
[ 74 ] T. H. Boyer, Phys. Rev. D 11: 790 (1975).
[ 75 ] P. Claverie, S. Diner, in O. Chalvet et al, Eds., Localization and Delocalization in Quantum Chemistry, Vol. II, p. 395 (Reidel, Dorchrecht, 1976).
[ 76 ] L. de la Pena, “Stochastic Electrodynamics: Its Development, Present Situation, and Perspectives”, in B. Gomez et al, Eds., Stochastic Processes Applied to Physics and other Related Fields, pp. 428-581 (Proceedings of the Escuela Lationamericana de Fisica held in Cali, Colombia, 21 June- 9 July, 1982; World Scientific, 1983).
[ 77 ] V. Spicka et al, in Theo. M. Nieuwenhuizen, Ed, Beyond the Quantum, pp. 247-270 (World Scientific, 2007).
[ 78 ] W. G. Tifft, Astrophysical Journal 206: 38 (1976); Astrophysical Journal 211: 31 (1977); Astrophysical Journal 382: 396 (1991).
[ 79 ] H. Arp, Quasars, Redshifts and Controversies, p. 112 (Interstellar Media, Berkeley, CA, 1987); Seeing Red: Redshifts, Cosmology and Academic Science, p. 199 (Apeiron, Montreal, Canada, 1998).
[ 80 ] P. F. Schewe & B. Stein, American Institute Physics, Physics News Update, No. 61 (3 Jan 1992); No. 104 (25 Nov 1992).
[ 81 ] News Editor, Scientific American (Dec 1992).
[ 82 ] J. Gribbin, New Scientist, p. 17 (9 Jul 1994)
[ 83 ] A. L. Peratt, IEEE Transactions on Plasma Science PS-14 (6): 763-778 (Dec 1986).
[ 84 ] A. L. Peratt, Physics of the Plasma Universe, Chap. 4, Section 4.6.3 (Springer-Verlag, 1992).
[ 85 ] B. J. Setterfield, “A Plasma Universe With Changing Zero Point Energy”, Proceedings of the NPA 8: 535-544 (2011); also “Reviewing a Plasma Universe with Zero Point Energy”, Journal of Vectorial Relativity 3 (3): 1-29 (Sep 2008).
[ 86 ] J. Malmivuo, R. Plonsey, Bioelectromagnetism, pp. 33, 39, 42 (Oxford University Press, New York, 1995).
[ 87 ] B. J. Setterfield, “Zero Point Energy and Gigantism in Fossils”, Proceedings of the NPA 8: 545-554 (2011).
[ 88 ] T. H. Boyer, Scientific American, pp. 70-78 (Aug 1985).
[ 89 ] B. J. Setterfield, “General Relativity and the Zero Point Energy,” Journal of Theoretics, extensive papers (15 Oct 2003).
[ 90 ] A. Eddington, Space, Time and Gravitation, p. 109 (Cambridge University Press, reprint 1987).
[ 91 ] M. Harwit, Astrophysical Concepts, p. 178 (Springer-Verlag, 1988).
[ 92 ] T. Van Flandern, in M. R. Edwards, Ed., Pushing Gravity, p. 94 (Apeiron, 2002).
[ 93 ] California Institute for Physics and Astrophysics, Questions and Answers, http://www.calphysics.org/questions.html; Y. Dobyns, A. Rueda, B. Haisch, Found. Phys. 30 (1): 59 (2000).
[ 94 ] B. Haisch, A. Rueda, H. Puthoff, The Sciences, p.26ff (Nov-Dec 1994)
[ 95 ] B. Haisch, quoted in New Scientist, pp. 22-25 (3 Feb 2001).
[ 96 ] P. E. Anderson, “Electric Scarring of the Earth’s Surface”, Proceedings of the NPA 9: this volume (July 2012).