Response concerning Jellison's criticisms

Request: Looking for information I encountered this forum. I cannot find out if the arguments (Jellison) are OK, but can you comment in short on this? Or have you posted an answer somewhere already? [Note: the forum URL sent to us no longer is valid; 2/8/12]

My article on "Quantized Redshifts and the Zero Point Energy," published by JVR in December of 2008, brings the entirely new approach to this whole situation. Jellison's comments are therefore out of date. There is now NO quantum change in sub-atomic particle masses. Everything depends on the behavior of Planck's constant, h, and the conservation of orbital angular momentum in atoms. What is now being proposed goes along the following lines (here I quote from an answer I gave to another enquirer):

"As the mass of subatomic particles smoothly increases with a smoothly increasing ZPE, the radius of any given atomic orbit will change. This happens because, as shown by Bohr's first equation for the orbiting electron, each orbit has a given amount of angular momentum which is proportional to Planck's constant, h. As the strength of the ZPE increases, so, too, does h. But angular momentum must be conserved in this process. In order for this to occur, the orbit radius must change. This change causes the light emitted from each atom to be more energetic or bluer. Thus as we look back in time to progressively more distant objects (that is objects whose light was emitted progressively earlier and earlier in the history of the cosmos), their light will be progressively redder. To astronomers, this is known as the redshift. This ZPE process has two possibilities; either it happened smoothly (in which case we would get a smoothly changing redshift), or it happened in jumps (so the redshift would be quantized). Observation indicates that the second option may be the one which is occurring. The evidence is there that the redshift may be quantized, but astronomers have been ignoring this for some considerable time because it knocks out one of the two legs which support the Big Bang proposition. The only viable alternative was mentioned by John Gribbin in New Scientist for 20th June 1985. This was that the redshift must be due to the behavior of atomic emitters within the various galaxies. This is the option which our research has validated."

As a result of this new approach, the orbit radius change is directly related to the behavior of Planck's constant, h, whether or not the redshift is quantized. If it is quantized, the orbit radius is only "catching up" with the change that has already occurred in h. As a consequence crystal sizes are not expected to change either at the quantum jump (if the redshift is indeed quantized as the observations suggest) or at any other time (if it is not). The reason given in my initial response to Jellison (explaining why thepressure counterbalances the orbit radius change) is now completely valid as the redshift change is DIRECTLY linked to h without any unilateral change in electron masses. It was this unexpected change in electron masses in the earlier presentation which allowed the problem that Jellison raised. Since this unilateral change no longer occurs, Jellison's comments are no longer valid.

Thanks for the explanation. I could follow the reasoning and the math. Below my pictorial interpretation of what you said.
So the quantized redshift remains. Your further remarks on the size of the quantum jump confirm what you have published before,
that a basic quantum jump of ± 2,68 km/sec applies, and that the quantum jumps become larger near the ʽedgeʼ of the universe,
as is probably the outcome of ongoing research. I suppose this nullifies Russell Humphreysʼ argument of quantized redshift being an artefact of galaxy cluster distribution.
You express the quantum steps in difference in wavelength, whereas in other papers the difference in the imaginary recession speed is used.
Is there a simple way to convert one into the other?
A last question: if atomic orbits decrease in size (= atomic sizes get smaller?), what reaction causes this in any material. Is there not a kind of shock effect?
Or is there a counter-action?
Your answers will clear up the whole problem for me.

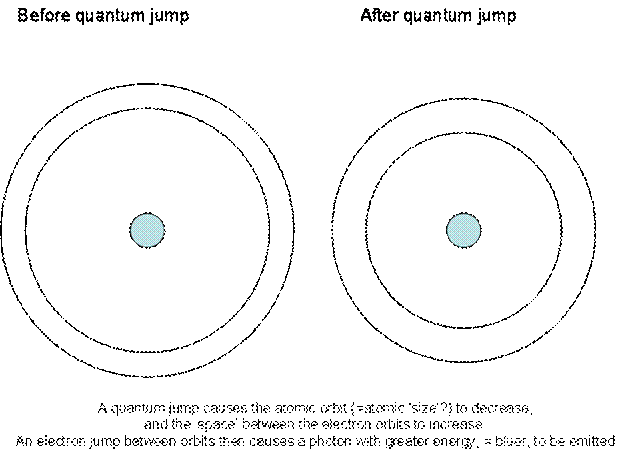
[words under diagram read as follows: A quantum jump causes the atomic orbit ( = atomic 'size'?) to decrease, and the space between the electron orbits to incrase. An electron jump between orbits then causes a photon with greater energy, = bluer, to be emitted.]

Setterfield:  As for your question - lets forget all you have ever learnt about the cause of the redshift!

Here is the new situation. The ZPE smoothly increases with time. Since Planck's constant is a measure of the strength of the ZPE, Planck's constant, (h), will also increase smoothly with time. Now subatomic masses, (m), are dependent upon the strength of the ZPE so that the mass is proportional to the square of the ZPE strength. Therefore, as the ZPE smoothly increases, subatomic masses smoothly increase in proportion to (h2). Now in any motion, the kinetic energy of the particle in motion must be conserved. That means that (0.5 mv2) must be conserved as the ZPE changes, where (v) is the velocity of the particle. So as (m) increases, the quantity (v2) must decrease in inverse proportion. That is (v2) is proportional to (1/m).. Since (1/m) is also proportional to (1/h2) this requires that (v2) is proportional to (1/h2). In other words, as the ZPE smoothly increases, the velocity of moving subatomic particles must decrease in such a way that (v) is proportional to (1/h).

What we have done here,is simply to apply the law of conservation of energy to moving subatomic particles. As the ZPE increases, their velocity decreases in inverse propoortion.. This must also apply in atomic orbits. So as the ZPE increases, the velocity of the electron gets less. That is the first part of the exercise.

The second part of the exercise is to note that Bohr's first equation for atomic orbits relates to orbital angular momentum. His equation reads:

mva = nh/(2p)

Here, orbit angular momentum is given by the left hand side of the equation (mva). We have already met (m) and (v) and (h). The new term here is (a), the orbit radius. The right hand side of the equation contains the term (n) which is the quantum number for the orbit. We can neglect that in this discussion or simply put it equal to one (1). What this equation says is that the orbital angular momentum is directly proportional to Planck's constant (h). So as (h) increases with increasing ZPE, the orbital angular momentum must also increase. From our above considerations, it must increase in such a way that (m) is proportional to (h2) and (v) is proportional to (1/h). In order for the equation to balance (or what amounts to the same thing, for all forces acting on the electron to balance), this requires the orbit radius (a) to be proportional to (1/h). In other words, as the strength of the ZPE increases with time, and (h) increases with time, the orbit radius decreases as (1/h).

AS this is looked at in detail with atomic structure and the math involved, it turns out that as atomic orbits decrease in radius, the separation between them actually increases. This means that there is a greater energy difference between the orbits, and so light emitted from an electron jumping from a higher to a lower orbit will actually become bluer with time because of this process.

The only question which now remains is whether or not this process will happen smoothly (in which case we get a smoothly decreasing redshift) or in quantum jumps (in which case we get a quantized redshift). The smoothly changing redshift needs no explanation. If it is the quantized redshift that is happening, the explanation goes as follows. Bohr's first equation noted that atomic orbits can only go in integer jumps of (h). It is possible that as (h) varies with the ZPE, atomic orbits can again only take up certain values of (h). The equations (20) to (26) in Quantized Redshifts and the Zero Point Energy discuss this possibility. What is done is to take the value of (h) when the ZPE had built up sufficiently after the creation event to allow atoms to form. That point is reached at the time of formation of the Cosmic Microwave Background Radiation. That value of (h) is labelled as (ho) in the paper. All changes then go in integer multiples of (ho) which can be labelled as (Nho) where (N) is an integer. The changes in wavelength are then in terms of [(4p ²) / (Nho)]. In this (ho) is a fixed quantity and (N) goes in steps of 1, 2, 3, 4, ...... So in the early universe, there were large steps because (N) was small, and in the later universe, (N) was becoming a very large number so that steps were very small [ such as the difference between [(4p ²)/34567] or (4p ²)/34568].

As far as Jellison is concerned now, his original argument is now invalid because a different model is being proposed.